题目内容
若等差数列{an}中,公差d>0,前n项和为Sn,且a2•a3=45,a1+a4=14,
(1)求数列{an}的通项公式;
(2)通过bn=
构造一个新数列{bn},是否存在一个非零常数c,使{bn}也为等差数列;
(3)在(2)中,求f(n)=
(n∈N*)的最大值.
(1)求数列{an}的通项公式;
(2)通过bn=
| Sn |
| n+c |
(3)在(2)中,求f(n)=
| bn |
| (n+30)•bn+1-62n |
考点:等差数列的性质,数列的函数特性
专题:综合题,等差数列与等比数列
分析:(1)等差数列{an}中,由公差d>0,a2•a3=45,a1+a4=14,利用等差数列的通项公式列出方程组,求出等差数列的首项和公差,由此能求出数列{an}的通项公式;
(2)求出bn=
,令c=
,可得结论;
(3)f(n)=
,确定其单调性,即可得出结论.
(2)求出bn=
| Sn |
| n+c |
| 1 |
| 2 |
(3)f(n)=
| bn |
| (n+30)•bn+1-62n |
解答:
解:(1)∵等差数列{an}中,公差d>0,a2•a3=45,a1+a4=14,
∴(a1+2d)(a1+2d)=45,a1+a1+3d=14
∵d>0,
∴a1=1,d=4,
∴an=a1+(n-1)d=1+4(n-1)=4n-3;
(2)Sn=
=2n(n-
),bn=
=
,
令c=-
,即得bn=2n,{bn}为等差数列.
∴存在c=-
,使{bn}也为等差数列.
(3)f(n)=
=
=
,
∴f(n)在[1,5]递增;f(n)在[6,+∞)n∈N*递减;
∴f(n)min=f(5)=f(6)=
.
∴(a1+2d)(a1+2d)=45,a1+a1+3d=14
∵d>0,
∴a1=1,d=4,
∴an=a1+(n-1)d=1+4(n-1)=4n-3;
(2)Sn=
| n(1+4n-3) |
| 2 |
| 1 |
| 2 |
| Sn |
| n+c |
2n(n-
| ||
| n+c |
令c=-
| 1 |
| 2 |
∴存在c=-
| 1 |
| 2 |
(3)f(n)=
| bn |
| (n+30)•bn+1-62n |
| n |
| (n+30)(n+1)-31n |
| 1 | ||
n+
|
∴f(n)在[1,5]递增;f(n)在[6,+∞)n∈N*递减;
∴f(n)min=f(5)=f(6)=
| 1 |
| 11 |
点评:本题考查了等差数列的通项公式与求和,考查了数列的函数特性,训练了配方法求函数最值,是中档题.

练习册系列答案
相关题目
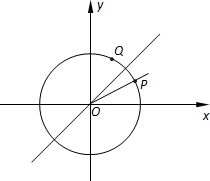 已知单位圆上两点P、Q关于直线y=x对称,且射线OP为终边的角的大小为x.另有两点M(a,-a)、N(-a,a),且f(x)=
已知单位圆上两点P、Q关于直线y=x对称,且射线OP为终边的角的大小为x.另有两点M(a,-a)、N(-a,a),且f(x)=