题目内容
已知函数f(x)=ex-ax(a为常数)的图象与y轴交于点A,曲线y=f(x)在点A处的切线斜率为-1.
(Ⅰ)求a的值及函数f(x)的极值
(Ⅱ)证明:当x>0时,x2<ex.
(Ⅲ)证明:对任意给定的正数c,总存在x0,使得当x∈(x0,+∞),恒有x2<cex.
(Ⅰ)求a的值及函数f(x)的极值
(Ⅱ)证明:当x>0时,x2<ex.
(Ⅲ)证明:对任意给定的正数c,总存在x0,使得当x∈(x0,+∞),恒有x2<cex.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)利用导数的几何意义求得a,再利用导数的符号变化可求得函数的极值;
(Ⅱ)构造函数g(x)=ex-x2,求出导数,利用(Ⅰ)问结论可得到函数的符号,从而判断g(x)的单调性,即可得出结论;
(Ⅲ)令x0=
,利用(Ⅱ)的结论,即得结论成立.
(Ⅱ)构造函数g(x)=ex-x2,求出导数,利用(Ⅰ)问结论可得到函数的符号,从而判断g(x)的单调性,即可得出结论;
(Ⅲ)令x0=
| 4 | ||
|
解答:
解:(Ⅰ)由f(x)=ex-ax得f′(x)=ex-a.
又f′(0)=1-a=-1,∴a=2,
∴f(x)=ex-2x,f′(x)=ex-2.
由f′(x)=0得x=ln2,
当x<ln2时,f′(x)<0,f(x)单调递减;
当x>ln2时,f′(x)>0,f(x)单调递增;
∴当x=ln2时,f(x)有极小值为f(ln2)=eln2-2ln2=2-ln4.
f(x)无极大值.
(Ⅱ)令g(x)=ex-x2,则g′(x)=ex-2x,
由(1)得,g′(x)=f(x)≥f(ln2)=eln2-2ln2=2-ln4>0,即g′(x)>0,
∴当x>0时,g(x)>g(0)>0,即x2<ex;
( III)对任意给定的正数c,取x0=
>0,
由( II)知,当x>0时,ex>x2,
∴ex=e
•e
>(
)2•(
)2,
当x>x0时,ex=e
•e
>(
)2•(
)2>
•(
)2=
,
因此,对任意给定的正数c,总存在x0,当x∈(x0,+∞)时,恒有x2<cex.
又f′(0)=1-a=-1,∴a=2,
∴f(x)=ex-2x,f′(x)=ex-2.
由f′(x)=0得x=ln2,
当x<ln2时,f′(x)<0,f(x)单调递减;
当x>ln2时,f′(x)>0,f(x)单调递增;
∴当x=ln2时,f(x)有极小值为f(ln2)=eln2-2ln2=2-ln4.
f(x)无极大值.
(Ⅱ)令g(x)=ex-x2,则g′(x)=ex-2x,
由(1)得,g′(x)=f(x)≥f(ln2)=eln2-2ln2=2-ln4>0,即g′(x)>0,
∴当x>0时,g(x)>g(0)>0,即x2<ex;
( III)对任意给定的正数c,取x0=
| 4 | ||
|
由( II)知,当x>0时,ex>x2,
∴ex=e
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
当x>x0时,ex=e
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| 4 |
| c |
| x |
| 2 |
| x2 |
| c |
因此,对任意给定的正数c,总存在x0,当x∈(x0,+∞)时,恒有x2<cex.
点评:本题主要考查基本初等函数的导数、导数的运算及导数的应用、综合性较强,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
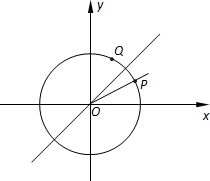 已知单位圆上两点P、Q关于直线y=x对称,且射线OP为终边的角的大小为x.另有两点M(a,-a)、N(-a,a),且f(x)=
已知单位圆上两点P、Q关于直线y=x对称,且射线OP为终边的角的大小为x.另有两点M(a,-a)、N(-a,a),且f(x)=