题目内容
已知△ABC的两顶点A、B分别是双曲线2x2-2y2=1的左、右焦点,且sinC是sinA,sinB的等差中项.
(1)求顶点C的轨迹T的方程;
(2)设P(-2,0),过点E(-
,0)作直线l交轨迹T于M、N两点,问∠MPN的大小是否为定值?证明你的结论.
(1)求顶点C的轨迹T的方程;
(2)设P(-2,0),过点E(-
| 2 |
| 7 |
考点:双曲线的简单性质
专题:计算题,解三角形,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)由条件可得|BC|+|AC|=2|AB|=4,根据椭圆的定义,即可求得点C的轨迹T的方程;
(2)设直线MN的方程,代入椭圆方程,利用韦达定理和向量知识,即可证得PM⊥PN.
(2)设直线MN的方程,代入椭圆方程,利用韦达定理和向量知识,即可证得PM⊥PN.
解答:
解:(1)由条件知双曲线2x2-2y2=1的左、右焦点A (-1,0 ),B (1,0 ),
且sinA+sinB=2sinC,∴|BC|+|AC|=2|AB|=4,
∴点C的轨迹是以A、B为焦点,长轴长2a=4的椭圆(不包括x轴上两点).
∴点C的轨迹T的方程是
+
=1 (x≠±2);
(2)设M (x1,y1)、N (x2,y2),直线MN:x=my+b,
由
,得 (3m2+4)y2+6mby+3b2-12=0,
∴y1+y2=-
,y1y2=
,
∵
=(x1+2,y1),
=(x2+2,y2)
∴
•
=( x1+2)(x2+2)+y1y2=(my1+b+2 ) (my2+b+2)+y1y2
=(m2+1)y1y2+m (b+2)(y1+y2)+(b+2)2,
=(m2+1)•
+m (b+2)•(-
)+(b+2)2,
由于直线l过点E(-
,0),则b=-
,代入上式,化简即可得到
•
=0,
则∠MPN的大小为定值,且为90°.
且sinA+sinB=2sinC,∴|BC|+|AC|=2|AB|=4,
∴点C的轨迹是以A、B为焦点,长轴长2a=4的椭圆(不包括x轴上两点).
∴点C的轨迹T的方程是
| x2 |
| 4 |
| y2 |
| 3 |
(2)设M (x1,y1)、N (x2,y2),直线MN:x=my+b,
由
|
∴y1+y2=-
| 6mb |
| 4+3m2 |
| 3b2-12 |
| 4+3m2 |
∵
| PM |
| PN |
∴
| PM |
| PN |
=(m2+1)y1y2+m (b+2)(y1+y2)+(b+2)2,
=(m2+1)•
| 3b2-12 |
| 4+3m2 |
| 6mb |
| 4+3m2 |
由于直线l过点E(-
| 2 |
| 7 |
| 2 |
| 7 |
| PM |
| PN |
则∠MPN的大小为定值,且为90°.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
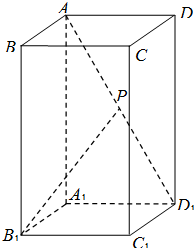 如图,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1的中点,求异面直线AA1与B1P所成的角(结果用反三角函数表示).
如图,已知ABCD-A1B1C1D1是底面为正方形的长方体,∠AD1A1=60°,AD1=4,点P是AD1的中点,求异面直线AA1与B1P所成的角(结果用反三角函数表示).