题目内容
已知直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R).圆C:(x-1)2+(y-2)2=25.
(1)求证:直线l恒过定点,并求出此定点;
(2)若直线l被圆C截得的线段的长度为4
,求实数m的值.
(1)求证:直线l恒过定点,并求出此定点;
(2)若直线l被圆C截得的线段的长度为4
| 6 |
考点:直线和圆的方程的应用
专题:计算题,直线与圆
分析:(1)直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R)整理,解方程组,即可得出结论;
(2)若直线l被圆C截得的线段的长度为4
,则圆心到直线的距离为1,即可求实数m的值.
(2)若直线l被圆C截得的线段的长度为4
| 6 |
解答:
解:(1)直线l:(2m+1)x+(m+1)y-7m-4=0(m∈R)可整理为:(2x+y-7)m+x+y-4=0⇒
⇒
故直线l恒过定点(3,1)…(6分)
(2)若直线l被圆C截得的线段的长度为4
,则圆心到直线的距离为1
即
=1⇒
=1⇒m=±
…(12分)
|
|
故直线l恒过定点(3,1)…(6分)
(2)若直线l被圆C截得的线段的长度为4
| 6 |
即
| |(2m+1)+2(m+1)-7m-4| | ||
|
| |3m+1| | ||
|
| 1 |
| 2 |
点评:本题考查直线恒过定点问题,考查点到直线间的距离公式,考查运算能力,属于中档题.

练习册系列答案
相关题目
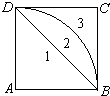 正方形ABCD被对角线BD和以A为圆心,AB为半径的圆弧
正方形ABCD被对角线BD和以A为圆心,AB为半径的圆弧 |
| DB |
| A、2:1:1 |
| B、1:2:1 |
| C、1:1:1 |
| D、2:2:1 |
已知双曲线的方程为
-
=1,点A,B在双曲线的右支上,线段AB经过双曲线的右焦点F2,|AB|=m,F1为另一焦点,则△ABF1的周长为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、2a+2m | B、a+m |
| C、4a+2m | D、2a+4m |
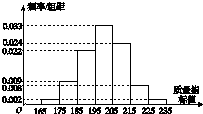 从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得到如图所示的频率分布直方图.
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得到如图所示的频率分布直方图.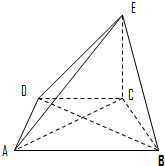 在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,EC⊥平面ABCD,CB=CD=CE.
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,EC⊥平面ABCD,CB=CD=CE.