题目内容
一圆过两椭圆
+
=1与
+
=1的交点,则该圆的方程是 .
| x2 |
| 9 |
| y2 |
| 4 |
| x2 |
| 4 |
| y2 |
| 9 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:直接利用已知条件,把椭圆的方程进行转化,再进行整合求得结果.
解答:
解:由已知
+
=1转化为:4x2+9y2=36①
同理:
+
=1转化为:9x2+4y2=36②
则①+②得:13x2+13y2=72,
圆的方程为:x2+y2=
,
故答案为:x2+y2=
.
| x2 |
| 9 |
| y2 |
| 4 |
同理:
| x2 |
| 4 |
| y2 |
| 9 |
则①+②得:13x2+13y2=72,
圆的方程为:x2+y2=
| 72 |
| 13 |
故答案为:x2+y2=
| 72 |
| 13 |
点评:本题考查的知识要点:利用椭圆的性质求圆的方程,利用对称性,属于基础题型.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
已知p:方程
+
=1所表示的曲线为焦点在x轴上的椭圆,q:|t-a|<2(a∈N),若p是q的充分不必要条件,则a取值范围为( )
| x2 |
| 3-t |
| y2 |
| t+1 |
| A、(-∞,1] |
| B、[-1,1] |
| C、[0,+∞) |
| D、(0,1) |
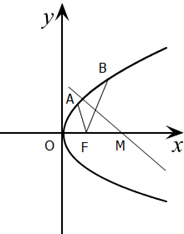 如图,已知抛物线C的顶点在原点,焦点点为圆x2+y2-2x=0的圆心,
如图,已知抛物线C的顶点在原点,焦点点为圆x2+y2-2x=0的圆心,