Question

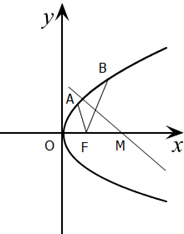如图，已知抛物线C的顶点在原点，焦点点为圆x²+y²-2x=0的圆心，
（Ⅰ）求抛物线C的方程；
（Ⅱ）设抛物线C上两个动点A、B满足|AF|+BF|=6线段AB的垂直平分线与x轴交于点M；
（1）求点M的坐标；
（2）当线段AB最长时，求△MAB的面积．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线的定义、性质与方程

分析：（Ⅰ）化圆的一般方程为标准方程，求出圆心坐标，则抛物线的焦点坐标可求，抛物线方程可求；
（Ⅱ）（1）设抛物线C上两个动点A、B的坐标，由|AF|+BF|=6结合焦半径可得AB的中点的坐标，把A、B的坐标代入抛物线方程，用点差法求得AB的斜率，则AB的垂直平分线方程可求，取y=0可得M点坐标；
（2）设出直线AB的方程，和抛物线方程联立，化为关于x的一元二次方程，由AB的横坐标的和为4求得斜率和截距的关系，再由弦长公式写出AB的长，利用二次函数求得最值及取得最值时的k值，得到AB的方程，由点到直线的距离求得M到AB的距离，代入三角形面积公式得答案．

解答： 解：（Ⅰ）把圆x²+y²-2x=0的方程化为：（x-1）²+y²=1，可知焦点坐标为（1，0），在x轴上，
那么抛物线方程为y²=2px，且

p

2

=1，则p=2，
∴抛物线C的方程是y²=4x；
（Ⅱ）（1）设A（x₁，y₁），B（x₂，y₂），
则y12=4x1，y22=4x2，
两式作差得：（y₁-y₂）（y₁+y₂）=4（x₁-x₂），
∴

y1-y2

x1-x2

=

4

y1+y2

，即AB的斜率为

4

y1+y2

．
由|AF|+BF|=6，则x₁+x₂+2=6，
∴x₁+x₂=4．
∴AB的中点坐标为（2，

y1+y2

2

），
∴AB的垂直平分线方程为y-

y1+y2

2

=-

y1+y2

4

(x-2)，
取y=0，得x=4．
∴点M的坐标为（4，0）；
（2）由题意可设AB的直线方程为y=kx+m（k≠0），
联立

y=kx+m y2=4x

，得k²x²+（2km-4）x+m²=0．
△=（2km-4）²-4k²m²=16-8km．
x1+x2=

4-2km

k2

=4，x1x2=

m2

k2

．
由

4-2km

k2

=4，得m=

2-2k2

k

．
∴|AB|=

1+k2

|x1-x2|=

1+k2

16-4• m2 k2

=

1+k2

16k2-4 (2-2k2)2 k2 k2

=4

- 1 k4 + 1 k2 +2

．
∴当

1

k2

=

1

2

，即k²=2时，|AB|有最大值为6．
此时AB的方程为：y=

2

x-

2

或y=-

2

x+

2

．
则M到直线AB的距离为d=

|4 2 - 2 |

3

=

6

．
∴S△AMB=

1

2

×6×

6

=3

6

．

点评：本题主要考查了直线与抛物线的位置关系的应用，直线与曲线联立，根据方程的根与系数的关系求解，是处理这类问题的最为常用的方法，但圆锥曲线的特点是计算量比较大，要求考生具备较强的运算推理的能力，是压轴题．