题目内容
一个袋子里装有7个除颜色和编号完全相同的球,其中红球4个,编号分别为1,2,3,4;白球3个,编号分别为2,3,4.从盒子中任取4个球,在取出的4个球中,红球编号的最大值设为X,则随机变量X的数学期望 .
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:由题意得随机变量X的所有可能取值为1,2,3,4.分别求出相应的概率,由此能求出随机变量X的分布列和数学期望.
解答:
解:由题意得随机变量X的所有可能取值为1,2,3,4.
P(X=1)=
=
,
P(X=2)=
=
,
P(X=3)=
=
,
P(X=4)=
=
,
所以随机变量X的分布列是
随机变量X的数学期望EX=1×
+2×
+3×
+4×
=
.
P(X=1)=
| ||
|
| 1 |
| 35 |
P(X=2)=
| ||
|
| 4 |
| 35 |
P(X=3)=
| ||
|
| 2 |
| 7 |
P(X=4)=
| ||
|
| 4 |
| 7 |
所以随机变量X的分布列是
| X | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
| 1 |
| 35 |
| 4 |
| 35 |
| 2 |
| 7 |
| 4 |
| 7 |
| 17 |
| 5 |
点评:本题考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A、{1,3,m},B={3,4},A∪B={1,2,3,4},则实数m是( )
| A、1 | B、2 | C、3 | D、4 |
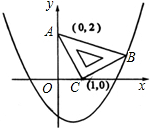 在平面直角坐标系中,现将一块等腰直角三角形ABC放在第一象限,斜靠在两坐标轴上,且点A(0,2),点C(1,0),如图所示:抛物线y=ax2-ax-2经过点B.
在平面直角坐标系中,现将一块等腰直角三角形ABC放在第一象限,斜靠在两坐标轴上,且点A(0,2),点C(1,0),如图所示:抛物线y=ax2-ax-2经过点B. 在长方体ABCD-A1B1C1D1中,AA1=1,AD=DC=
在长方体ABCD-A1B1C1D1中,AA1=1,AD=DC=