题目内容
 在长方体ABCD-A1B1C1D1中,AA1=1,AD=DC=
在长方体ABCD-A1B1C1D1中,AA1=1,AD=DC=| 3 |
| 1 |
| 3 |
考点:二面角的平面角及求法
专题:空间位置关系与距离
分析:建立空间直角坐标系,求出相关点的坐标,求出平面A1CD,平面QCD的法向量,利用空间向量的数量积,即可求得平面QDC与平面A1DC所成锐二面角.
解答:
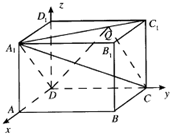 解:建立空间直角坐标系,
解:建立空间直角坐标系,
则D(0,0,0),C(0,
,0),A1(
,0,1),C1(0,
,1).
∵C1Q=
C1A1,
∴Q(
,
,1).
设平面A1CD,平面QCD的一个法向量分别为
=(x1,y1,z1),
=(x2,y2,z2)
由
⇒
令x1=1,∴z1=-
∴
=(1,0,-
)
由
⇒
令x2=1,∴z1=-
.
∴
=(1,0,-
),
cos<
,
>=
=
=
,
∴<
,
>=
.
即平面QDC与平面A1DC所成锐二面角为
.
 解:建立空间直角坐标系,
解:建立空间直角坐标系,则D(0,0,0),C(0,
| 3 |
| 3 |
| 3 |
∵C1Q=
| 1 |
| 3 |
∴Q(
| ||
| 3 |
2
| ||
| 3 |
设平面A1CD,平面QCD的一个法向量分别为
| n |
| m |
由
|
|
令x1=1,∴z1=-
| 3 |
∴
| n |
| 3 |
由
|
|
令x2=1,∴z1=-
| ||
| 3 |
∴
| m |
| ||
| 3 |
cos<
| n |
| m |
| n•m | ||||
|
|
| 1+1 | ||||
2×
|
| ||
| 2 |
∴<
| n |
| m |
| π |
| 6 |
即平面QDC与平面A1DC所成锐二面角为
| π |
| 6 |
点评:本题考查二面角的余弦值的求法,考查空间位置关系与距离,解题时要认真审题,注意向量法的合理运用,属于中档题.

练习册系列答案
相关题目
设集合U={1,2,3,4,5,6,7},M={2,4,7},则∁UM=( )
| A、U |
| B、{1,2,6} |
| C、{1,3,5,6} |
| D、{1,3,5} |
已知某个几何体的三视图如图,则这个几何体的表面积为( )
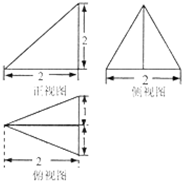

A、4+
| ||
B、4+2
| ||
| C、6 | ||
| D、8 |
若不等式(a-a2)•(x2+1)+x≤0对一切x∈[(0,2]恒成立,则a的取值范围为( )
A、(-∞,
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、(-∞,
|
