题目内容
19．
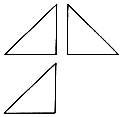在体积为V的球内有一个多面体，该多面体的三视图是如图所示的三个斜边都是$\sqrt{2}$的等腰直角三角形，则V的最小值是（ ）| A． | $4\sqrt{3π}$ | B． | $\frac{{\sqrt{3}π}}{2}$ | C． | 3π | D． | 12π |
分析 由多面体的三视图知该多面体是如图所示的三棱锥P-ABC，PA⊥底面ABC，AB⊥BC，PA=AB=BC=1，当球是这个三棱锥的外接球时，其体积V最小，将这个三棱锥补成正方体，即可得出结论．
解答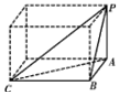 
解：由多面体的三视图知该多面体是如图所示的三棱锥P-ABC，PA⊥底面ABC，AB⊥BC，PA=AB=BC=1，当球是这个三棱锥的外接球时，其体积V最小，将这个三棱锥补成正方体，其外接球的直径就是正方体的对角线PC=$\sqrt{3}$，
∴V=$\frac{4}{3}π•（\frac{\sqrt{3}}{2}）^{3}$=$\frac{\sqrt{3}}{2}π$，
故选：B．
点评 本题考查球的体积，考查线面垂直，正确构造正方体是关键．
练习册系列答案
相关题目
9．已知$3\overrightarrow a+4\overrightarrow b+5\overrightarrow c=0$，且$|\overrightarrow a|=|\overrightarrow b|=|\overrightarrow c|=1$，则$\overrightarrow b•（\overrightarrow a+\overrightarrow c）$等于（ ）
| A． | -$\frac{4}{5}$ | B． | -$\frac{3}{5}$ | C． | 0 | D． | $\frac{3}{5}$ |
7．已知平面向量$\overrightarrow a$与$\overrightarrow b$的夹角等于$\frac{π}{3}$，若|$\overrightarrow a$|=2，|$\overrightarrow b$|=3，则|2$\overrightarrow a$-3$\overrightarrow b$|=（ ）
| A． | $\sqrt{57}$ | B． | $\sqrt{61}$ | C． | 57 | D． | 61 |
14．如图所给的程序运行结果为S=41，那么判断框中应填入的关于k的条件是（ ）
| A． | k≥6 | B． | k≥5 | C． | k＞6 | D． | k＞5 |
4．空间四边形ABCD的四个顶点都在同一球面上，E、F分别是AB、CD的中点，且EF⊥AB，EF⊥CD，若AB=8，CD=EF=4，则该球的半径等于（ ）
| A． | $\frac{{65\sqrt{2}}}{16}$ | B． | $\frac{{65\sqrt{2}}}{8}$ | C． | $\frac{{\sqrt{65}}}{2}$ | D． | $\sqrt{65}$ |
11．椭圆的对称轴为坐标轴，若长、短轴之和为18，焦距为6，那么椭圆的方程为（ ）
| A． | $\frac{x^2}{9}+\frac{y^2}{16}=1$ | B． | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | ||
| C． | $\frac{x^2}{25}+\frac{y^2}{16}=1$或$\frac{x^2}{16}+\frac{y^2}{25}=1$ | D． | $\frac{x^2}{16}+\frac{y^2}{25}=1$ |
8．已知 y=f （ x ） 是定义在 R 上的偶函数，且当 x∈（-∞，0），f （ x ）+xf'（ x ）＜0成立（ f'（ x ） 是函数 f （ x） 的导数），若 a=$\frac{1}{2}$f （log2$\sqrt{2}$ ），b=（ln 2 ） f （ln 2 ），c=2f （-2 ），则 a，b，c 的大小关系是（ ）
| A． | a＞b＞c | B． | b＞a＞c | C． | c＞a＞b | D． | a＞c＞b |
9．已知集合A={x|x2-2x-3＞0}，集合B={x∈Z|x2≤4x}，则∁RA∩B=（ ）
| A． | {x|0≤x≤3} | B． | {-1，0，1，2，3} | C． | {0，1，2，3} | D． | {1，2} |