题目内容
11.椭圆的对称轴为坐标轴,若长、短轴之和为18,焦距为6,那么椭圆的方程为( )| A. | $\frac{x^2}{9}+\frac{y^2}{16}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | ||
| C. | $\frac{x^2}{25}+\frac{y^2}{16}=1$或$\frac{x^2}{16}+\frac{y^2}{25}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{25}=1$ |
分析 利用已知条件列出方程,求出长轴长,短轴长,然后求解椭圆方程.
解答 解:椭圆的对称轴为坐标轴,若长、短轴之和为18,焦距为6,
可得:a+b=9,c=3,a2-b2=9,解得a=5,b=4.
所求的椭圆方程为:$\frac{x^2}{25}+\frac{y^2}{16}=1$或$\frac{x^2}{16}+\frac{y^2}{25}=1$.
故选:C.
点评 本题考查椭圆的简单性质以及椭圆方程的求法,考查计算能力.

练习册系列答案
相关题目
19.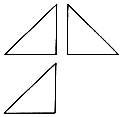 在体积为V的球内有一个多面体,该多面体的三视图是如图所示的三个斜边都是$\sqrt{2}$的等腰直角三角形,则V的最小值是( )
在体积为V的球内有一个多面体,该多面体的三视图是如图所示的三个斜边都是$\sqrt{2}$的等腰直角三角形,则V的最小值是( )
 在体积为V的球内有一个多面体,该多面体的三视图是如图所示的三个斜边都是$\sqrt{2}$的等腰直角三角形,则V的最小值是( )
在体积为V的球内有一个多面体,该多面体的三视图是如图所示的三个斜边都是$\sqrt{2}$的等腰直角三角形,则V的最小值是( )| A. | $4\sqrt{3π}$ | B. | $\frac{{\sqrt{3}π}}{2}$ | C. | 3π | D. | 12π |
16.一个长方体被一个平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为( )

| A. | 36 | B. | 48 | C. | 64 | D. | 72 |
20. 如图所示的程序框图,若输入x,k,b,p的值分别 为1,-2,9,3,则输出x的值为( )
如图所示的程序框图,若输入x,k,b,p的值分别 为1,-2,9,3,则输出x的值为( )
 如图所示的程序框图,若输入x,k,b,p的值分别 为1,-2,9,3,则输出x的值为( )
如图所示的程序框图,若输入x,k,b,p的值分别 为1,-2,9,3,则输出x的值为( )| A. | -29 | B. | -5 | C. | 7 | D. | 19 |