题目内容
9.已知集合A={x|x2-2x-3>0},集合B={x∈Z|x2≤4x},则∁RA∩B=( )| A. | {x|0≤x≤3} | B. | {-1,0,1,2,3} | C. | {0,1,2,3} | D. | {1,2} |
分析 根据题意,解x2-2x-3>0可得集合A,由补集的意义可得∁RA={x|-1≤x≤3},解x2≤4x可得集合B,由交集的意义计算∁RA∩B即可得答案.
解答 解:根据题意,x2-2x-3>0⇒x<-1或x>3,
则A={x|x2-2x-3>0}={x|x<-1或x>3},
则∁RA={x|-1≤x≤3},
x2≤4x⇒0≤x≤4,
B={x∈Z|x2≤4x}={x∈Z|0≤x≤4}={0,1,2,3,4},
则∁RA∩B={0,1,2,3};
故选:C.
点评 本题考查集合的混合运算,关键是正确求出集合A、B.

练习册系列答案
相关题目
19.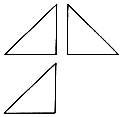 在体积为V的球内有一个多面体,该多面体的三视图是如图所示的三个斜边都是$\sqrt{2}$的等腰直角三角形,则V的最小值是( )
在体积为V的球内有一个多面体,该多面体的三视图是如图所示的三个斜边都是$\sqrt{2}$的等腰直角三角形,则V的最小值是( )
 在体积为V的球内有一个多面体,该多面体的三视图是如图所示的三个斜边都是$\sqrt{2}$的等腰直角三角形,则V的最小值是( )
在体积为V的球内有一个多面体,该多面体的三视图是如图所示的三个斜边都是$\sqrt{2}$的等腰直角三角形,则V的最小值是( )| A. | $4\sqrt{3π}$ | B. | $\frac{{\sqrt{3}π}}{2}$ | C. | 3π | D. | 12π |
20. 如图所示的程序框图,若输入x,k,b,p的值分别 为1,-2,9,3,则输出x的值为( )
如图所示的程序框图,若输入x,k,b,p的值分别 为1,-2,9,3,则输出x的值为( )
 如图所示的程序框图,若输入x,k,b,p的值分别 为1,-2,9,3,则输出x的值为( )
如图所示的程序框图,若输入x,k,b,p的值分别 为1,-2,9,3,则输出x的值为( )| A. | -29 | B. | -5 | C. | 7 | D. | 19 |
17.执行如图程序框图,则输出的S值为( )


| A. | 0 | B. | -1 | C. | $-\frac{1}{2}$ | D. | $-\frac{3}{2}$ |
9.以下是某地搜集到的新房屋的销售价格y与房屋的面积x的数据:
数据对应的散点图如图所示;
(1)求线性回归方程.(参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
(参考数据 $\overline{x}$=$\frac{1}{5}$$\sum_{i=1}^{5}$xi=109,$\sum_{i=1}^{5}$(xi-$\overline{x}$)2=1570,$\sum_{i=1}^{5}$(xi-$\overline{x}$)(yi-$\overline{y}$)=311.2)
(2)据(1)的结果估计当房屋面积为150m2时的销售价格.
| 房屋面积(m2) | 115 | 110 | 80 | 135 | 105 |
| 销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(1)求线性回归方程.(参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
(参考数据 $\overline{x}$=$\frac{1}{5}$$\sum_{i=1}^{5}$xi=109,$\sum_{i=1}^{5}$(xi-$\overline{x}$)2=1570,$\sum_{i=1}^{5}$(xi-$\overline{x}$)(yi-$\overline{y}$)=311.2)
(2)据(1)的结果估计当房屋面积为150m2时的销售价格.