题目内容
4．空间四边形ABCD的四个顶点都在同一球面上，E、F分别是AB、CD的中点，且EF⊥AB，EF⊥CD，若AB=8，CD=EF=4，则该球的半径等于（ ）| A． | $\frac{{65\sqrt{2}}}{16}$ | B． | $\frac{{65\sqrt{2}}}{8}$ | C． | $\frac{{\sqrt{65}}}{2}$ | D． | $\sqrt{65}$ |
分析 由题意，球心O必在EF上，则OF2+22=R2=（4-OF）2+42，即可得出结论．
解答 解：由题意，球心O必在EF上，则OF2+22=R2=（4-OF）2+42，∴OF=$\frac{7}{2}$，R=$\frac{\sqrt{65}}{2}$．
故选C．
点评 本题考查球的半径的求解，考查方程思想，比较基础．
练习册系列答案
名校课堂系列答案
相关题目
14．运行如图所示的程序框图，若输入的实数为2，则输出的n为（ ）
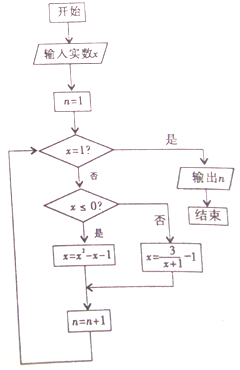
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
12．已知某几何体的三视图（单位：cm）如图所示，则该几何体的体积是（ ）
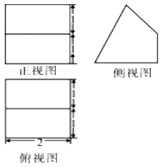
| A． | 3cm3 | B． | 5cm3 | C． | 4cm3 | D． | 6cm3 |
19．
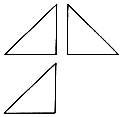在体积为V的球内有一个多面体，该多面体的三视图是如图所示的三个斜边都是$\sqrt{2}$的等腰直角三角形，则V的最小值是（ ）
在体积为V的球内有一个多面体，该多面体的三视图是如图所示的三个斜边都是$\sqrt{2}$的等腰直角三角形，则V的最小值是（ ）| A． | $4\sqrt{3π}$ | B． | $\frac{{\sqrt{3}π}}{2}$ | C． | 3π | D． | 12π |
9．不等式3≤|5-2x|＜9的解集为（ ）
| A． | [-2，1）∪[4，7） | B． | （-2，1]∪[4，7] | C． | （-2，1]∪（4，7） | D． | （-2，1]∪[4，7） |
16．一个长方体被一个平面截去一部分后，所剩几何体的三视图如图所示，则该几何体的体积为（ ）
| A． | 36 | B． | 48 | C． | 64 | D． | 72 |
将三项式（x2+x+1）n展开，当n=0，1，2，3，…时，得到以下等式：