题目内容
9.已知$3\overrightarrow a+4\overrightarrow b+5\overrightarrow c=0$,且$|\overrightarrow a|=|\overrightarrow b|=|\overrightarrow c|=1$,则$\overrightarrow b•(\overrightarrow a+\overrightarrow c)$等于( )| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | 0 | D. | $\frac{3}{5}$ |
分析 根据题意,求出$\overrightarrow{b}$•$\overrightarrow{c}$=-$\frac{4}{5}$,$\overrightarrow{a}$•$\overrightarrow{b}$=0,即可计算$\overrightarrow b•(\overrightarrow a+\overrightarrow c)$的值.
解答 解:$3\overrightarrow a+4\overrightarrow b+5\overrightarrow c=0$,且$|\overrightarrow a|=|\overrightarrow b|=|\overrightarrow c|=1$,
∴-3$\overrightarrow{a}$=4$\overrightarrow{b}$+5$\overrightarrow{c}$,
∴9${\overrightarrow{a}}^{2}$=16${\overrightarrow{b}}^{2}$+40$\overrightarrow{b}$$•\overrightarrow{c}$+25${\overrightarrow{c}}^{2}$,
∴9=16+40$\overrightarrow{b}$$•\overrightarrow{c}$+25,
∴$\overrightarrow{b}$•$\overrightarrow{c}$=-$\frac{4}{5}$;
又-5$\overrightarrow{c}$=3$\overrightarrow{a}$+4$\overrightarrow{b}$,
∴25c2=9${\overrightarrow{a}}^{2}$+24$\overrightarrow{a}$•$\overrightarrow{b}$+16${\overrightarrow{b}}^{2}$,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=0;
∴$\overrightarrow b•(\overrightarrow a+\overrightarrow c)$=$\overrightarrow{b}$$•\overrightarrow{a}$+$\overrightarrow{b}$$•\overrightarrow{c}$=0+(-$\frac{4}{5}$)=-$\frac{4}{5}$.
故选:A.
点评 本题考查了平面向量的数量积运算问题,是基础题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
| A. | $y=±\sqrt{2}x$ | B. | y=±2x | C. | $y=±\frac{{\sqrt{2}}}{2}x$或y=$±\sqrt{2}x$ | D. | $y=±\frac{1}{2}x$ |
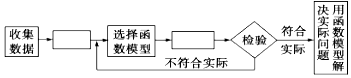
| A. | 整理数据、求函数关系式 | B. | 画散点图、进行模型修改 | ||
| C. | 画散点图、求函数关系式 | D. | 整理数据、进行模型修改 |
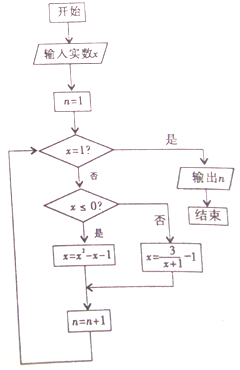
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
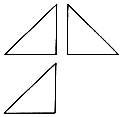 在体积为V的球内有一个多面体,该多面体的三视图是如图所示的三个斜边都是$\sqrt{2}$的等腰直角三角形,则V的最小值是( )
在体积为V的球内有一个多面体,该多面体的三视图是如图所示的三个斜边都是$\sqrt{2}$的等腰直角三角形,则V的最小值是( )| A. | $4\sqrt{3π}$ | B. | $\frac{{\sqrt{3}π}}{2}$ | C. | 3π | D. | 12π |