题目内容
7.已知平面向量$\overrightarrow a$与$\overrightarrow b$的夹角等于$\frac{π}{3}$,若|$\overrightarrow a$|=2,|$\overrightarrow b$|=3,则|2$\overrightarrow a$-3$\overrightarrow b$|=( )| A. | $\sqrt{57}$ | B. | $\sqrt{61}$ | C. | 57 | D. | 61 |
分析 利用本题主要考查两个向量的数量积的定义求得$\overrightarrow{a}•\overrightarrow{b}$的值,再根据|2$\overrightarrow a$-3$\overrightarrow b$|=$\sqrt{{(2\overrightarrow{a}-3\overrightarrow{b})}^{2}}$,计算求得结果.
解答 解:平面向量$\overrightarrow a$与$\overrightarrow b$的夹角等于$\frac{π}{3}$,若|$\overrightarrow a$|=2,|$\overrightarrow b$|=3,则$\overrightarrow{a}•\overrightarrow{b}$=2•3•cos$\frac{π}{3}$=3,
则|2$\overrightarrow a$-3$\overrightarrow b$|=$\sqrt{{(2\overrightarrow{a}-3\overrightarrow{b})}^{2}}$=$\sqrt{{4\overrightarrow{a}}^{2}-12\overrightarrow{a}•\overrightarrow{b}+{9\overrightarrow{b}}^{2}}$=$\sqrt{16+81-36}$=$\sqrt{61}$.
故选:B.
点评 本题主要考查两个向量的数量积的定义,求向量的模的方法,属于基础题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
17.设双曲线的虚轴长为2,焦距为$2\sqrt{3}$,则双曲线的渐近线方程为( )
| A. | $y=±\sqrt{2}x$ | B. | y=±2x | C. | $y=±\frac{{\sqrt{2}}}{2}x$或y=$±\sqrt{2}x$ | D. | $y=±\frac{1}{2}x$ |
12.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )
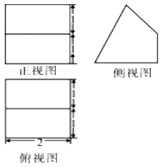

| A. | 3cm3 | B. | 5cm3 | C. | 4cm3 | D. | 6cm3 |
19.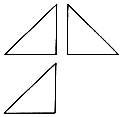 在体积为V的球内有一个多面体,该多面体的三视图是如图所示的三个斜边都是$\sqrt{2}$的等腰直角三角形,则V的最小值是( )
在体积为V的球内有一个多面体,该多面体的三视图是如图所示的三个斜边都是$\sqrt{2}$的等腰直角三角形,则V的最小值是( )
 在体积为V的球内有一个多面体,该多面体的三视图是如图所示的三个斜边都是$\sqrt{2}$的等腰直角三角形,则V的最小值是( )
在体积为V的球内有一个多面体,该多面体的三视图是如图所示的三个斜边都是$\sqrt{2}$的等腰直角三角形,则V的最小值是( )| A. | $4\sqrt{3π}$ | B. | $\frac{{\sqrt{3}π}}{2}$ | C. | 3π | D. | 12π |
16.一个长方体被一个平面截去一部分后,所剩几何体的三视图如图所示,则该几何体的体积为( )

| A. | 36 | B. | 48 | C. | 64 | D. | 72 |
17.执行如图程序框图,则输出的S值为( )


| A. | 0 | B. | -1 | C. | $-\frac{1}{2}$ | D. | $-\frac{3}{2}$ |