题目内容
曲线y=ln（2-x）在点（1，0）处的切线方程是 ．
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：求出原函数的导函数，得到y′|x=1=-1，然后由直线方程的点斜式得曲线y=ln（2-x）在点（1，0）处的切线方程．
解答：
解：由y=ln（2-x），得y′=
=
，
∴y′|x=1=-1．
即曲线y=ln（2-x）在点（1，0）处的切线的斜率为-1．
∴曲线y=ln（2-x）在点（1，0）处的切线方程为y-0=-1×（x-1），
整理得：y=-x+1．
故答案为：y=-x+1．
| -1 |
| 2-x |
| 1 |
| x-2 |
∴y′|x=1=-1．
即曲线y=ln（2-x）在点（1，0）处的切线的斜率为-1．
∴曲线y=ln（2-x）在点（1，0）处的切线方程为y-0=-1×（x-1），
整理得：y=-x+1．
故答案为：y=-x+1．
点评：本题考查利用导数研究曲线上某点处的切线方程，曲线上过某点处的切线的斜率，就是函数在该点处的导数值，是中档题．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
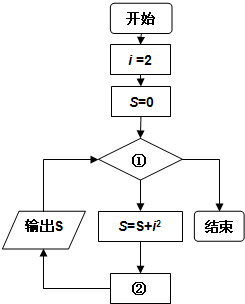如图是表示输出22，22+42，22+42+62，…，22+42+62+…+20042的值的过程的一个程序框图，那么在图中①、②处应分别填上（ ）| A、i≤2014，i=i+2 |
| B、i≤1007，i=i+2 |
| C、i≤2014，i=i+1 |
| D、i≤1007，i=i+1 |
设集合M={x|2x＜
}，N={x|-2≤x≤3}，则M∩N=（ ）
| 1 |
| 2 |
| A、[-2，1） |
| B、[-2，-l） |
| C、（-1，3] |
| D、[-2，3] |