题目内容
18.在面积为S的三角形ABC的边AB上任意取一点P,则三角形PBC的面积大于$\frac{S}{4}$的概率为$\frac{3}{4}$.分析 首先分析题目求在面积为S的△ABC的边AB上任取一点P,则△PBC的面积大于$\frac{S}{4}$的概率,可借助于画图求解的方法,然后根据图形分析出基本的事件空间与事件的几何度量是什么.再根据几何关系求解出它们的比例即可
解答 解:记事件A={△PBC的面积大于$\frac{S}{4}$的概率},
基本事件空间是线段AB的长度,(如图)
因为 S△PBC>$\frac{S}{4}$,则有 $\frac{1}{2}$BC•PE$≥\frac{1}{4}×\frac{1}{2}$BC•AD;
化简记得到:$\frac{PE}{AD}≥\frac{1}{4}$,
因为PE平行AD则由三角形的相似性 $\frac{BP}{AB}$$≥\frac{1}{4}$;
所以,事件A的几何度量为线段AP的长度,
因为AP=$\frac{3}{4}$AB,
所以P(A)=$\frac{AP}{AB}$.
故△PBC的面积大于$\frac{S}{4}$的概率的概率为 $\frac{3}{4}$;
故答案为:$\frac{3}{4}$.
点评 解决有关几何概型的问题的关键是认清基本事件空间是指面积还是长度或体积,并且熟练记忆有关的概率公式.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
9.设变量x,y满足约束条件$\left\{\begin{array}{l}x-2y+1≤0\\ x+y-5≤0\\ 4x-2y+1≥0\end{array}\right.$,若目标函数z=mx-y取得最大值的最优解有无数个,则m=( )
| A. | $\frac{1}{2}$ | B. | -1 | C. | 2 | D. | $-1或\frac{1}{2}$ |
6.在2016年巴西里约奥运会期间,6名游泳队员从左至右排成一排合影留念,最左边只能排甲或乙,最右端不能排甲,则不同的排法种数为( )
| A. | 216 | B. | 108 | C. | 432 | D. | 120 |
13.已知命题p:?x∈R,x2-mx+1=0,q:?x∈R,ex-m>0,若¬p∧q为真,则实数m的取值范围是( )
| A. | [-2,2] | B. | (-2,0] | C. | (-2,0) | D. | [0,2] |
3.下列函数中,既是偶函数又在(0,+∞)上单调递增的是( )
| A. | y=lgx | B. | y=cosx | C. | y=|x| | D. | y=sinx |
10.某研究小组在电脑上进行人工降雨模拟实验,准备用A、B、C三种人工降雨方式分别对甲,乙,丙三地实施人工降雨,其实验统计结果如下
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,且不考虑洪涝灾害,请根据统计数据:
(Ⅰ)求甲、乙、丙三地都恰为中雨的概率;
(Ⅱ)考虑不同地区的干旱程度,当雨量达到理想状态时,能缓解旱情,若甲、丙地需中雨即达到理想状态,乙地必须是大雨才达到理想状态,记“甲,乙,丙三地中缓解旱情的个数”为随机变量X,求X的分布列和数学期望.
| 方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验次数 |
| A | 甲 | 2次 | 6次 | 4次 | 12次 |
| B | 乙 | 3次 | 6次 | 3次 | 12次 |
| C | 丙 | 2次 | 2次 | 8次 | 12次 |
(Ⅰ)求甲、乙、丙三地都恰为中雨的概率;
(Ⅱ)考虑不同地区的干旱程度,当雨量达到理想状态时,能缓解旱情,若甲、丙地需中雨即达到理想状态,乙地必须是大雨才达到理想状态,记“甲,乙,丙三地中缓解旱情的个数”为随机变量X,求X的分布列和数学期望.
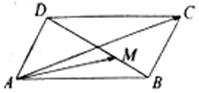 如图,平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,$\overrightarrow{DM}=2\overrightarrow{MB}$,则$\overrightarrow{AC}•\overrightarrow{AM}$=4.
如图,平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,$\overrightarrow{DM}=2\overrightarrow{MB}$,则$\overrightarrow{AC}•\overrightarrow{AM}$=4.