题目内容
10.已知向量$\overrightarrow a=(cosα,sinα)$,$\overrightarrow b=(cosβ,sinβ)$,且$α-β=\frac{2π}{3}$,则$\overrightarrow a$与$\overrightarrow a+\overrightarrow b$的夹角为( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
分析 设向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,根据向量的夹角公式公式计算即可.
解答 解:∵向量$\overrightarrow a=(cosα,sinα)$,$\overrightarrow b=(cosβ,sinβ)$,且$α-β=\frac{2π}{3}$,设向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ
∴$\overrightarrow a$•($\overrightarrow a+\overrightarrow b$)=${\overrightarrow{a}}^{2}$+$\overrightarrow{a}•\overrightarrow{b}$=1+cosθ,
|$\overrightarrow a+\overrightarrow b$|2=${\overrightarrow{a}}^{2}$+2$\overrightarrow{a}•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=2+2cosθ,
∴cos<$\overrightarrow a$,$\overrightarrow a+\overrightarrow b$>=$\frac{\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})}{\overrightarrow{|a|}•|\overrightarrow{a}+\overrightarrow{b}|}$=$\frac{1+cosθ}{2+2cosθ}$=$\frac{1}{2}$,
∵夹角的范围0~π,
∴$\overrightarrow a$与$\overrightarrow a+\overrightarrow b$的夹角$\frac{π}{3}$.
故选:A
点评 本题主要考查了向量的坐标运算和数量积的运算,属于基础题

| A. | f(x)=3-x | B. | f(x)=(x-1)2 | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=x2+2x |
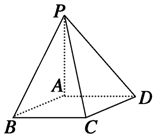
| A. | 平面ABCD | B. | 平面PBC | C. | 平面PAD | D. | 平面PBC |
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{4}$ | D. | $\frac{1}{4}$ |
| A. | $1+\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $2+\sqrt{2}$ | D. | 0 |