题目内容
函数f(x)=
,若f(a)<f(8-a),则a的取值范围是( )
|
| A、(-∞,4) |
| B、(-4,4) |
| C、(-4,0) |
| D、(0,4) |
考点:分段函数的应用
专题:函数的性质及应用
分析:实际上是一个分段函数构造产生的不等式(组),分成两种情况讨论即可.
解答:
解:因为当x>0时,-x<0,所以f(x)=x2+4x,f(-x)=x2+4x,所以此时f(-x)=f(x);
同理当x<0时,也有f(-x)=f(x)成立;
当x=0时,亦有f(-x)=f(0)=0,综上,函数f(-x)=f(x)恒成立,所以函数f(x)是偶函数.
结合图象可知,该函数以y轴为对称轴,且y轴左边递减,右边递增,所以离y轴越近,函数值越小.
所以由f(a)<f(8-a)得|a|<|8-a|,即a2<(8-a)2,解得a<4.
故选:A.
同理当x<0时,也有f(-x)=f(x)成立;
当x=0时,亦有f(-x)=f(0)=0,综上,函数f(-x)=f(x)恒成立,所以函数f(x)是偶函数.
结合图象可知,该函数以y轴为对称轴,且y轴左边递减,右边递增,所以离y轴越近,函数值越小.
所以由f(a)<f(8-a)得|a|<|8-a|,即a2<(8-a)2,解得a<4.
故选:A.
点评:此题体现了分段函数分段处理的基本原则,考查了分类讨论的思想.

练习册系列答案
相关题目
已知全集U={x∈Z|x2-9x+8<0},M={3,5,6},N={x|x2-9x+20=0},则集合{2,7}为( )
| A、M∪N |
| B、M∩N |
| C、∁U(M∪N) |
| D、∁U(M∩N) |
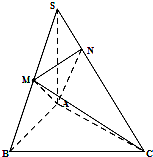 如图,在三棱锥S-ABC中,SA⊥底面ABC,点B为以AC为直径的圆上任意一动点,且SA=AB,点M是SB的中点,AN⊥SC且交SC于点N.
如图,在三棱锥S-ABC中,SA⊥底面ABC,点B为以AC为直径的圆上任意一动点,且SA=AB,点M是SB的中点,AN⊥SC且交SC于点N.