题目内容
在△ABC中,a,b,c是角A,B,C对应的边,向量m=(a+b,c),n=(a+b,-c),且m·n=( +2)ab.
+2)ab.
(1)求角C;
(2)函数f(x)=2sin(A+B)cos2(ωx)-cos(A+B)sin(2ωx)-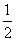 (ω>0)的相邻两个极值的横坐标分别为x0-
(ω>0)的相邻两个极值的横坐标分别为x0-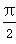 ,x0,求f(x)的单调递减区间.
,x0,求f(x)的单调递减区间.
解:(1)因为m=(a+b,c),n=(a+b,-c),m·n=( +2)ab,所以a2+b2-c2=
+2)ab,所以a2+b2-c2= ab,故cos C=
ab,故cos C=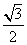 ,
,
∵0<C<π,∴C=
(2)f(x)=2sin(A+B)cos2(ωx)-cos(A+B)sin(2ωx)-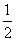
=2sin Ccos2(ωx)+cos Csin(2ωx)-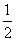
=cos2(ωx)+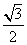 sin(2ωx)-
sin(2ωx)-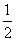
=sin
因为相邻两个极值的横坐标分别为x0- ,x0,所以f(x)的最小正周期为T=π,ω=1,
,x0,所以f(x)的最小正周期为T=π,ω=1,
 k∈Z.
k∈Z.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 ,
, ,则
,则 等于
等于  ( B )
( B ) B.
B.
 D.
D.
 上单调递减,则ω的取值范围是( )
上单调递减,则ω的取值范围是( ) D.(0,2]
D.(0,2]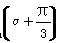 +sin α=-
+sin α=-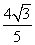 ,-
,-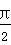 <α<0,则cos
<α<0,则cos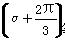 等于( )
等于( )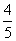 B.-
B.-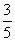
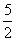 ,a2+a4=
,a2+a4= ,则
,则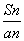 =( )
=( )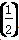 的值为________.
的值为________.