题目内容
17.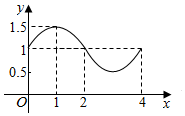 函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(0)+f(1)+f(2)+…+f(2013)+f(2014)+f(2015)+f(2016)的值分别为( )
函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(0)+f(1)+f(2)+…+f(2013)+f(2014)+f(2015)+f(2016)的值分别为( )| A. | f(x)=$\frac{1}{2}$sin2πx+1,S=2016 | B. | f(x)=$\frac{1}{2}$sin2πx+1,S=2016$\frac{1}{2}$ | ||
| C. | f(x)=$\frac{1}{2}$sin$\frac{π}{2}$x+1,S=2017$\frac{1}{2}$ | D. | f(x)=$\frac{1}{2}$sin$\frac{π}{2}$x+1,S=2017 |
分析 由函数图象和解析式的关系,逐步求解可得解析式,由函数的周期性可得函数值.
解答 解:由图象知A=1.5-1=0.5,T=4=$\frac{2π}{ω}$,∴ω=$\frac{π}{2}$,b=1,
∴f(x)=0.5sin($\frac{π}{2}$x+φ)+1,
由f(x)的图象过点(1,1.5)得0.5sin($\frac{π}{2}$+φ)+1=1.5,
∴cosφ=1,∴φ=2kπ,k∈Z,取k=0得φ=0,
∴f(x)=0.5sin($\frac{π}{2}$x)+1,
∴f(0)+f(1)+f(2)+f(3)=(0.5sin0+1)+(0.5sin$\frac{π}{2}$+1)+(0.5sinπ+1)+(0.5sin$\frac{3π}{2}$+1)=4,
2016=4×504+0,∴S=4×504+f(2016)=2016+f(0)=2017.
故选:D.
点评 本题考查三角函数的图象和解析式,涉及函数的周期性和函数的值,属中档题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
8.若复数z满足关系$z•\overline{z}$=1,则z对应的复平面的点的轨迹是( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 直线 |
7.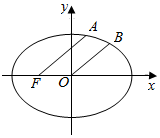 如图,已知椭圆方程为$\frac{{x}^{2}}{2}$+y2=1,F是其左焦点,A、B在椭圆上,满足FA∥OB且|FA|:|OB|=3:2,则点A的横坐标为( )
如图,已知椭圆方程为$\frac{{x}^{2}}{2}$+y2=1,F是其左焦点,A、B在椭圆上,满足FA∥OB且|FA|:|OB|=3:2,则点A的横坐标为( )
 如图,已知椭圆方程为$\frac{{x}^{2}}{2}$+y2=1,F是其左焦点,A、B在椭圆上,满足FA∥OB且|FA|:|OB|=3:2,则点A的横坐标为( )
如图,已知椭圆方程为$\frac{{x}^{2}}{2}$+y2=1,F是其左焦点,A、B在椭圆上,满足FA∥OB且|FA|:|OB|=3:2,则点A的横坐标为( )| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
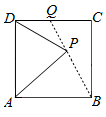 如图,在边长为2的正方形ABCD中,点Q边CD上一个动点,$\overrightarrow{CQ}$=λ$\overrightarrow{QD}$,点P为线段BQ(含端点)上一个动点,若λ=1,则$\overrightarrow{PA}$•$\overrightarrow{PD}$的取值范围为[$\frac{4}{5}$,4].
如图,在边长为2的正方形ABCD中,点Q边CD上一个动点,$\overrightarrow{CQ}$=λ$\overrightarrow{QD}$,点P为线段BQ(含端点)上一个动点,若λ=1,则$\overrightarrow{PA}$•$\overrightarrow{PD}$的取值范围为[$\frac{4}{5}$,4].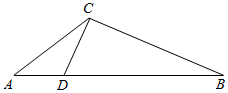 如图,在△ABC 中,点D在边 AB上,且$\frac{AD}{DB}$=$\frac{1}{3}$.记∠ACD=α,
如图,在△ABC 中,点D在边 AB上,且$\frac{AD}{DB}$=$\frac{1}{3}$.记∠ACD=α,