题目内容
12.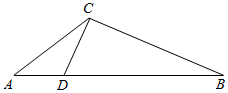 如图,在△ABC 中,点D在边 AB上,且$\frac{AD}{DB}$=$\frac{1}{3}$.记∠ACD=α,
如图,在△ABC 中,点D在边 AB上,且$\frac{AD}{DB}$=$\frac{1}{3}$.记∠ACD=α,∠BCD=β.
(Ⅰ)求证:$\frac{AC}{BC}$=$\frac{sinβ}{3sinα}$
(Ⅱ)若α=$\frac{π}{6}$,β=$\frac{π}{2}$,AB=$\sqrt{19}$,求BC 的长.
分析 (I)分别在△ACD和△BCD中使用正弦定理,根据sin∠ADC=sin∠BDC和$\frac{AD}{DB}=\frac{1}{3}$得出结论.
(II)利用(I)的结论可知$\frac{AC}{BC}=\frac{2}{3}$,在△ABC中使用余弦定理解出BC.
解答 解:(Ⅰ)在△ACD中,由正弦定理得:$\frac{AC}{sin∠ADC}=\frac{AD}{sinα}$,
在△BCD中,由正弦定理得:$\frac{BC}{sin∠BDC}=\frac{BD}{sinβ}$,
∵∠ADC+∠BDC=π,∴sin∠ADC=sin∠BDC,
∵$\frac{AD}{DB}=\frac{1}{3}$,∴$\frac{AC}{BC}=\frac{sinβ}{3sinα}$.
(Ⅱ)∵$α=\frac{π}{6}$,$β=\frac{π}{2}$,
∴$\frac{AC}{BC}=\frac{sinβ}{3sinα}=\frac{2}{3}$,∠ACB=α+β=$\frac{2π}{3}$.
设AC=2k,BC=3k,k>0,由余弦定理得:AB2=AC2+BC2-2AC•BC•cos∠ACB,
即$19=4{k^2}+9{k^2}-2•2k•3k•cos\frac{2π}{3}$,
解得k=1,∴BC=3.
点评 本题考查了正弦定理,余弦定理,属于中档题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
2.已知α,β是△ABC的两锐角,且$(sinα+1)(1-\frac{1}{sinα})>(cosβ+1)(1-\frac{1}{cosβ})$,则△ABC的形状为( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
20.已知平面直角坐标系中两个定点E(3,2),F(-3,2),如果对于常数λ,在函数y=|x+2|+|x-2|-4,(x∈[-4,4])的图象上有且只有6个不同的点P,使得$\overrightarrow{PE}$$•\overrightarrow{PF}$=λ成立,那么λ的取值范围是( )
| A. | (-5,-$\frac{9}{5}$) | B. | (-$\frac{9}{5}$,11) | C. | (-$\frac{9}{5}$,-1) | D. | (-5,11) |
7.已知函数y=sin(2x+φ)在x=$\frac{π}{6}$处取得最大值,则函数y=cos(2x+φ)的图象( )
| A. | 关于点($\frac{π}{6}$,0)对称 | B. | 关于点($\frac{π}{3}$,0)对称 | ||
| C. | 关于直线x=$\frac{π}{6}$对称 | D. | 关于直线x=$\frac{π}{3}$对称 |
17.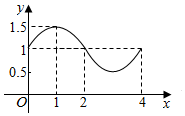 函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(0)+f(1)+f(2)+…+f(2013)+f(2014)+f(2015)+f(2016)的值分别为( )
函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(0)+f(1)+f(2)+…+f(2013)+f(2014)+f(2015)+f(2016)的值分别为( )
 函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(0)+f(1)+f(2)+…+f(2013)+f(2014)+f(2015)+f(2016)的值分别为( )
函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式和S=f(0)+f(1)+f(2)+…+f(2013)+f(2014)+f(2015)+f(2016)的值分别为( )| A. | f(x)=$\frac{1}{2}$sin2πx+1,S=2016 | B. | f(x)=$\frac{1}{2}$sin2πx+1,S=2016$\frac{1}{2}$ | ||
| C. | f(x)=$\frac{1}{2}$sin$\frac{π}{2}$x+1,S=2017$\frac{1}{2}$ | D. | f(x)=$\frac{1}{2}$sin$\frac{π}{2}$x+1,S=2017 |
4.若函数f(x)=2sin2x的图象向右平移φ(0<φ<$\frac{π}{2}$)个单位后得到函数g(x)的图象,若对满足|f(x1)-g(x2)|=4的x1、x2,有|x1-x2|的最小值为$\frac{π}{6}$,则φ=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
2.已知命题p:?x∈R,cosx=$\frac{5}{4}$;命题q:?x∈R,2x+1>0.则下列正确的是( )
| A. | p∧q是真命题 | B. | p∧(﹁q)是真命题 | C. | ﹁p∧q是真命题 | D. | ﹁p∧﹁q是假命题 |