题目内容
在无穷数列{an}中,a1=1,对于任意n∈N*,都有an∈N*,an<an+1.设m∈N*,记使得an≤m成立的n的最大值为bm.
(Ⅰ)设数列{an}为1,3,5,7,…,写出b1,b2,b3的值;
(Ⅱ)若{an}为等比数列,且a2=2,求b1+b2+b3+…+b50的值;
(Ⅲ)若{bn}为等差数列,求出所有可能的数列{an}.
(Ⅰ)设数列{an}为1,3,5,7,…,写出b1,b2,b3的值;
(Ⅱ)若{an}为等比数列,且a2=2,求b1+b2+b3+…+b50的值;
(Ⅲ)若{bn}为等差数列,求出所有可能的数列{an}.
考点:等比数列的性质
专题:综合题,等差数列与等比数列
分析:(Ⅰ)根据使得an≤m成立的n的最大值为bm,即可写出b1,b2,b3的值;
(Ⅱ)确定b1=1,b2=b3=2,b4=b5=b6=b7=3,b8=b9=…=b15=4,b16=b17=…=b31=5,b32=b33=…=b50=6,分组求和,即可求b1+b2+b3+…+b50的值;
(Ⅲ)若{bn}为等差数列,先判断an≥n,再证明an≤n,即可求出所有可能的数列{an}.
(Ⅱ)确定b1=1,b2=b3=2,b4=b5=b6=b7=3,b8=b9=…=b15=4,b16=b17=…=b31=5,b32=b33=…=b50=6,分组求和,即可求b1+b2+b3+…+b50的值;
(Ⅲ)若{bn}为等差数列,先判断an≥n,再证明an≤n,即可求出所有可能的数列{an}.
解答:
解:(Ⅰ)an≤1,则b1=1,an≤2,则b2=1,an≤3,则b3=3.…(3分)
(Ⅱ)因为{an}为等比数列,a1=1,a2=2,
所以an=2n-1,…(4分)
因为使得an≤m成立的n的最大值为bm,
所以b1=1,b2=b3=2,b4=b5=b6=b7=3,b8=b9=…=b15=4,b16=b17=…=b31=5,b32=b33=…=b50=6,…(6分)
所以b1+b2+b3+…+b50=243.…(8分)
(Ⅲ)解:由题意,得1=a1<a2<…<an<…,
得an≥n.…(9分)
又因为使得an≤m成立的n的最大值为bm,使得an≤m+1成立的n的最大值为bm+1,
所以b1=1,bm≤bm+1.…(10分)
设a2=k,则k≥2.
假设k>2,即a2=k>2,
则当n≥2时,an>2;当n≥3时,an≥k+1.
所以b2=1,bk=2.
因为{bn}为等差数列,
所以公差d=b2-b1=0,
所以bn=1,.
这与bk=2(k>2)矛盾,
所以a2=2.…(11分)
又因为a1<a2<…<an<…,
所以b2=2,
由{bn}为等差数列,得bn=n.…(12分)
因为使得使得an≤m成立的n的最大值为bm,
所以an≤n,
由an≥n,得an=n.…(13分)
(Ⅱ)因为{an}为等比数列,a1=1,a2=2,
所以an=2n-1,…(4分)
因为使得an≤m成立的n的最大值为bm,
所以b1=1,b2=b3=2,b4=b5=b6=b7=3,b8=b9=…=b15=4,b16=b17=…=b31=5,b32=b33=…=b50=6,…(6分)
所以b1+b2+b3+…+b50=243.…(8分)
(Ⅲ)解:由题意,得1=a1<a2<…<an<…,
得an≥n.…(9分)
又因为使得an≤m成立的n的最大值为bm,使得an≤m+1成立的n的最大值为bm+1,
所以b1=1,bm≤bm+1.…(10分)
设a2=k,则k≥2.
假设k>2,即a2=k>2,
则当n≥2时,an>2;当n≥3时,an≥k+1.
所以b2=1,bk=2.
因为{bn}为等差数列,
所以公差d=b2-b1=0,
所以bn=1,.
这与bk=2(k>2)矛盾,
所以a2=2.…(11分)
又因为a1<a2<…<an<…,
所以b2=2,
由{bn}为等差数列,得bn=n.…(12分)
因为使得使得an≤m成立的n的最大值为bm,
所以an≤n,
由an≥n,得an=n.…(13分)
点评:本题考查等比数列的性质,考查学生对题意的理解,考查学生分析解决问题的能力,有难度.

练习册系列答案
相关题目
从装有2个红球和2个黒球的口袋内任取2个球,下面属于互斥而不对立的两个事件是( )
| A、至少有一个黒球与都是红球 |
| B、至少有一个黒球与都是黒球 |
| C、至少有一个黒球与恰有1个红球 |
| D、恰有2个黒球与恰有2个红球 |
在△ABC中,角A、B、C所对的边分别为a、b、c,若acosB+bcosA=csinC且a=b,则角B等于( )
| A、30° | B、45° |
| C、60° | D、90° |
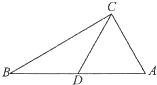 如图在△ABC中,已知∠A=
如图在△ABC中,已知∠A=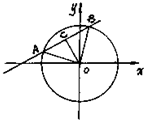 已知直线:y=k(x+2)与圆O:x2+y2=4相交于A、B两点,O是坐标原点,三角形ABO的面积为S.
已知直线:y=k(x+2)与圆O:x2+y2=4相交于A、B两点,O是坐标原点,三角形ABO的面积为S.