题目内容
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB中点,且△PMB为正三角形.
(1)求证:DM∥平面APC;
(2)求证:平面ABC⊥平面APC;
(3)若BC=4,AB=20,求三棱锥D-BCM的体积.

解:
(1)∵M为AB中点,D为PB中点,
∴DM∥AP,又DM⊄平面APC,AP⊂平面APC.
∴DM∥平面APC.
(2)∵△PMB为正三角形,且D为PB中点,
 ∴MD⊥PB,又由(1)知MD∥AP,
∴MD⊥PB,又由(1)知MD∥AP,
∴AP⊥PB
又已知AP⊥PC,∴AP⊥平面PBC,
∴AP⊥BC,又∵AC⊥BC
∴BC⊥平面APC
∴平面ABC⊥平面APC.
(3)∵AB=20,∴MP=10,∴PB=10
又BC=4,PC= =2
=2
∴S△BDC= S△PBC=
S△PBC= PC·BC=
PC·BC= ×4×2
×4×2
=2
又MD= AP=
AP=
 =5
=5
∴VD-BCM=VM-BCD= S△BDC·DM=
S△BDC·DM= ×2
×2 ×5
×5
=10 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 +sin x,其导函数记为f′(x),则f(2 013)+f′(2 013)+f(-2 013)-f′(-2 013)=________.
+sin x,其导函数记为f′(x),则f(2 013)+f′(2 013)+f(-2 013)-f′(-2 013)=________. 中,角
中,角 、
、 、
、 的对边分别是a、b、c。已知
的对边分别是a、b、c。已知 ,则
,则 是 ( )
是 ( ) :
: 及直线
及直线 ,
, 被
被 时,则
时,则 ( )
( ) B
B  C
C  D
D 
 ,则侧面与底面所成的二面角等于_______________。
,则侧面与底面所成的二面角等于_______________。 
 B. 16
B. 16 C. 9
C. 9
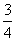 B.
B.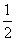 <a<
<a<