Question

如图，圆O的半径OC垂直于直径AB，弦CD交半径OA于E，过D的切线与BA的延长线于M．
（Ⅰ）已知∠BMD=40°，求∠MED：；
（Ⅱ）设圆O的半径为1，MD=

3

，求MA及CD的长．

Answer 1

考点：与圆有关的比例线段

专题：直线与圆

分析：（Ⅰ）由已知条件推导出∠MDE=∠MED，由此利用∠BMD=40°，能求出∠MED．
（Ⅱ）由已知条件求出OM=2，从而能求出MA=1，OE=2-

3

，由此利用余弦定理能求出CD的长．

解答： 解：（Ⅰ）连接OD，∵OD=OC，∴∠OCD=∠ODC，
∵MD切圆O于D，∴∠ODM=∠ODC+∠MDE=90°，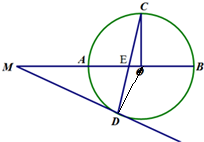
∵OC⊥AB，∴∠OCD+∠OEC=90°，∴∠OEC=∠MDE，
∵∠OEC=∠MED，∴∠MDE=∠MED，
∵∠BMD=40°，∴∠MED=

1

2

(180°-40°)=70°．
（Ⅱ）∵∠ODM=90°，OD=1，MD=

3

，∴OM=2，
∵OA=1，∴MA=OM-OA=1，
∵ME=MD=

3

，∴OE=OM-ME=2-

3

，
∵OC⊥OE，OC=1，
∴CE²=1+（2-

3

）²=8-4

3

=（

6

-

2

）²，
∴CE=

6

-

2

，
∵DE=

4+4-2×2×2×cos40°

=2

2-2cos40°

，
∴CD=CE+DE=

6

-

2

+2

2-2cos40°

．

点评：本题考查角的求法和线段长的求法，是中档题，解题时要注意勾股定理和余弦定理的合理运用．