题目内容
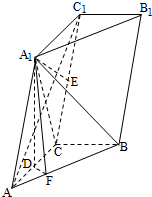如图，三棱柱ABC-A1B1C1中，点A1在平面ABC内的射影D在AC上，∠ACB=90°，BC=1，AC=CC1=2．（Ⅰ）证明：AC1⊥A1B；
（Ⅱ）设直线AA1与平面BCC1B1的距离为
| 3 |
考点：用空间向量求平面间的夹角,直线与平面垂直的性质,二面角的平面角及求法
专题：空间位置关系与距离
分析：（Ⅰ）由已知数据结合三垂线定理可得；
（Ⅱ）作辅助线可证∠A1FD为二面角A1-AB-C的平面角，解三角形由反三角函数可得．
（Ⅱ）作辅助线可证∠A1FD为二面角A1-AB-C的平面角，解三角形由反三角函数可得．
解答：
解：（Ⅰ）∵A1D⊥平面ABC，A1D?平面AA1C1C，
∴平面AA1C1C⊥平面ABC，又BC⊥AC
∴BC⊥平面AA1C1C，连结A1C，
由侧面AA1C1C为菱形可得AC1⊥A1C，
由三垂线定理可得AC1⊥A1B；
（Ⅱ）∵BC⊥平面AA1C1C，BC?平面BCC1B1，
∴平面AA1C1C⊥平面BCC1B1，
作A1E⊥CC1，E为垂足，可得A1E⊥平面BCC1B1，
又直线AA1∥平面BCC1B1，
∴A1E为直线AA1与平面BCC1B1的距离，即A1E=
，
∵A1C为∠ACC1的平分线，∴A1D=A1E=
，
作DF⊥AB，F为垂足，连结A1F，
由三垂线定理可得A1F⊥AB，
∴∠A1FD为二面角A1-AB-C的平面角，
由AD=
=1可知D为AC中点，
∴DF=
×
=
，
∴tan∠A1FD=
=
，
∴二面角A1-AB-C的大小为arctan
∴平面AA1C1C⊥平面ABC，又BC⊥AC
∴BC⊥平面AA1C1C，连结A1C，
由侧面AA1C1C为菱形可得AC1⊥A1C，
由三垂线定理可得AC1⊥A1B；
（Ⅱ）∵BC⊥平面AA1C1C，BC?平面BCC1B1，
∴平面AA1C1C⊥平面BCC1B1，
作A1E⊥CC1，E为垂足，可得A1E⊥平面BCC1B1，
又直线AA1∥平面BCC1B1，
∴A1E为直线AA1与平面BCC1B1的距离，即A1E=
| 3 |
∵A1C为∠ACC1的平分线，∴A1D=A1E=
| 3 |
作DF⊥AB，F为垂足，连结A1F，
由三垂线定理可得A1F⊥AB，
∴∠A1FD为二面角A1-AB-C的平面角，
由AD=
| AA12-A1D2 |
∴DF=
| 1 |
| 2 |
| AC×BC |
| AB |
| ||
| 5 |
∴tan∠A1FD=
| A1D |
| DF |
| 15 |
∴二面角A1-AB-C的大小为arctan
| 15 |
点评：本题考查二面角的求解，作出并证明二面角的平面角是解决问题的关键，属中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知集合A={-1，2，3}，B={y|y=x3，x∈A}，则A∩B=（ ）
| A、{0} | B、{1} |
| C、{-1} | D、{0，1} |
设a1，a2，a3均为正数，λ1＜λ2＜λ3，则函数f（x）=
+
+
的两个零点分别位于区间（ ）
| a1 |
| x-λ1 |
| a2 |
| x-λ2 |
| a3 |
| x-λ3 |
| A、（-∞，λ1）∪（λ1，λ2）内 |
| B、（λ1，λ2）∪（λ2，λ3）内 |
| C、（λ2，λ3）∪（λ3，+∞）内 |
| D、（-∞，λ1）∪（λ3，+∞）内 |
直三棱柱ABC-A1B1C1中，∠BCA=90°，M，N分别是A1B1，A1C1的中点，BC=CA=CC1，则BM与AN所成角的余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|