题目内容
 “世界睡眠日”定在每年的3月21日,2009年的世界睡眠日主题是“科学管理睡眠”,以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站于2009年3月13日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时),共有2000人参加调查,现将数据整理分组后如题中表格所示.
“世界睡眠日”定在每年的3月21日,2009年的世界睡眠日主题是“科学管理睡眠”,以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站于2009年3月13日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时),共有2000人参加调查,现将数据整理分组后如题中表格所示.(1)求出表中空白处的数据,并将表格补充完整;
(2)画出频率分布直方图;
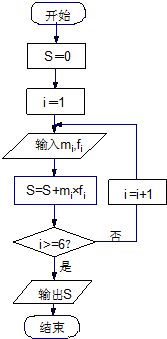
(3)为了对数据举行分析,采用了计算机辅助计算.分析中一部分计算见算法流程图,求输出的S值.
| 序号(i) | 分组睡眠时间 | 组中值(mi) | 频数 (人数) | 频率(fi) |
| 1 | [4,5) | 4.5 | 80 | |
| 2 | [5,6) | 5.5 | 520 | 0.26 |
| 3 | [6,7) | 6.5 | 600 | 0.30 |
| 4 | [7,8) | 7.5 | ||
| 5 | [8,9) | 8.5 | 200 | 0.10 |
| 6 | [9,10] | 9.5 | 40 | 0.02 |
考点:程序框图,频率分布直方图
专题:概率与统计,算法和程序框图
分析:(1)根据频率分布表求出样本数据在[4,5)的频率,在[7,8)的频数和频率;
(2)根据频率分布表,画出频率分布直方图;
(3)模拟程序框图的运行过程,得出该程序运行的结果是输入m1、f1的值后,由赋值语句S=S+m1•f1求和,进而得出输出的S值.
(2)根据频率分布表,画出频率分布直方图;
(3)模拟程序框图的运行过程,得出该程序运行的结果是输入m1、f1的值后,由赋值语句S=S+m1•f1求和,进而得出输出的S值.
解答:
 解:(1)样本数据在[4,5)的频率是
解:(1)样本数据在[4,5)的频率是
=0.04;
样本数据在[7,8)的频数是2000-(80+520+600+200+40)=560;
对应的频率是
=0.28;
∴频率分布表中空白处应填的数据是0.04、560、0.28;…(3分)
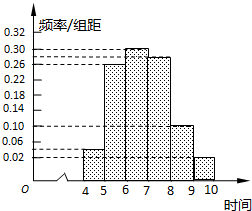
(2)根据频率分布表,画出频率分布直方图,如图所示;…(9分)
(3)首先要理解直到型循环结构图的含义.
输入m1、f1的值后,由赋值语句:S=S+m1•f1可知,
流程图进入一个求和状态:
令ai=mi•fi(i=1,2,…,6),前i项的和为Ti,
即:T6=4.5×0.04+5.5×0.26+6.5×0.30+7.5×0.28+8.5×0.10+9.5×0.02=6.70;
∴输出的S为6.70.…(14分)
 解:(1)样本数据在[4,5)的频率是
解:(1)样本数据在[4,5)的频率是| 80 |
| 2000 |
样本数据在[7,8)的频数是2000-(80+520+600+200+40)=560;
对应的频率是
| 560 |
| 2000 |
∴频率分布表中空白处应填的数据是0.04、560、0.28;…(3分)
(2)根据频率分布表,画出频率分布直方图,如图所示;…(9分)
(3)首先要理解直到型循环结构图的含义.
输入m1、f1的值后,由赋值语句:S=S+m1•f1可知,
流程图进入一个求和状态:
令ai=mi•fi(i=1,2,…,6),前i项的和为Ti,
即:T6=4.5×0.04+5.5×0.26+6.5×0.30+7.5×0.28+8.5×0.10+9.5×0.02=6.70;
∴输出的S为6.70.…(14分)
点评:本题考查了频率分布直方图与程序框图的应用问题,解题时应根据频率分布表画出分布直方图,模拟程序的运行过程,得出程序运行的结果,是综合题.

练习册系列答案
相关题目
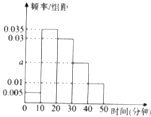 经统计,某校学生上学路程所需要时间全部介于0与50之间(单位:分钟),现从在校学生中随机抽取100人,按上学所需时间分组如下:第1组(0,10],第2组(10,20],第3组(20,30],第4组(30,40],第5组(40,50],得到如图所示的频率分布直方图.
经统计,某校学生上学路程所需要时间全部介于0与50之间(单位:分钟),现从在校学生中随机抽取100人,按上学所需时间分组如下:第1组(0,10],第2组(10,20],第3组(20,30],第4组(30,40],第5组(40,50],得到如图所示的频率分布直方图.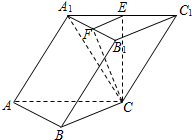 在斜三棱柱ABC-A1B1C1中,已知侧面ACC1A1⊥底面ABC,A1C=C1C,E,F分别是A1C1、A1B1的中点.
在斜三棱柱ABC-A1B1C1中,已知侧面ACC1A1⊥底面ABC,A1C=C1C,E,F分别是A1C1、A1B1的中点.