题目内容

9．已知直线l：y=kx与椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$交于A、B两点，其中右焦点F的坐标为（c，0），且AF与BF垂直，则椭圆C的离心率的取值范围为（　　）
A．$[{\frac{{\sqrt{2}}}{2}，1}）$B．$（{0，\frac{{\sqrt{2}}}{2}}]$C．$（{\frac{{\sqrt{2}}}{2}，1}）$D．$（{0，\frac{{\sqrt{2}}}{2}}）$

分析 由AF与BF垂直，运用直角三角形斜边的中线即为斜边的一半，再由椭圆的性质可得c＞b，结合离心率公式和a，b，c的关系，即可得到所求范围．

解答 解：由AF与BF垂直，
运用直角三角形斜边的中线即为斜边的一半，
可得||OA|=|OF|=c，
由|OA|＞b，即c＞b，可得c2＞b2=a2-c2，
即有c2＞$\frac{1}{2}$a2，
可得$\frac{\sqrt{2}}{2}$＜e＜1．
故选：C．

点评 本题考查椭圆的离心率的范围，注意运用直角三角形斜边上中线的性质，以及离心率公式和弦长的性质，考查运算能力，属于中档题．

练习册系列答案
相关题目
12．在△0AB中，$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，若|$\overrightarrow{a}$+2$\overrightarrow{b}$|=|$\overrightarrow{a}$-2$\overrightarrow{b}$|，则△OAB是直角三角形．
20．运行下面的程序框图，输出的结果为（　　）
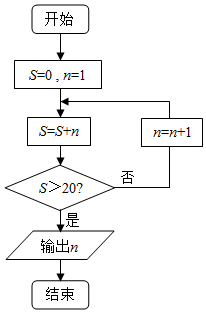
A．5B．6C．7D．8
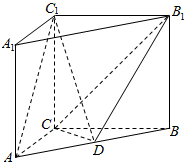17．如图，在三棱柱ABC-A1B1C1中，CC1⊥底面ABC，AC=BC=CC1=2，AC⊥BC，点D是AB的中点．
（1）求异面直线AC1与BB1所成的角；
（2）求四面体B1C1CD的体积．
4．已知正实数x，y满足xy+x+y=17，则x+2y+3的最小值为12．
14．“数列{an}成等比数列”是“数列{lgan+1}成等差数列”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
1．已知数列{an}的前n项和Sn=n2，若Sm是am与am+1的等差中项，则正整数m的值为（　　）
A．1B．2C．4D．8
18．已知在△ABC中，AB=4，AC=6，BC=$\sqrt{7}$，其外接圆的圆心为O，则$\overrightarrow{AO}$$•\overrightarrow{BC}$10．
19．执行如图所示的程序框图，则输出的S为（　　）
A．$\frac{1}{3}$B．2C．-$\frac{1}{2}$D．-3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网