��Ŀ����
17��ijҽѧ������������֬�����������������������о��õ�һ������������ݣ�����Excel���������$\widehat{y}$=0.577x-0.448��xΪ�˵����䣬y����λ��%��Ϊ����֬����������������Ϊ37�������˵������˵����ȷ���ǣ�������| A�� | ����Ϊ37���������֬��������Ϊ20.90% | |
| B�� | ����Ϊ37���������֬������Ϊ21.01% | |
| C�� | ����Ϊ37�����Ⱥ�еĴ��˵�����֬������Ϊ20.90% | |
| D�� | ����Ϊ37��Ĵֵ�������֬������Ϊ31.50% |
���� ��x=37����$\widehat{y}$=0.577x-0.448���㼴�ɵô𰸣�
��� �⣺�����⣬$\widehat{y}$=0.577x-0.448��
��x=37ʱ���ɵ�y=20.9%��
����Ϊ����Ϊ37�����Ⱥ�еĴ��˵�����֬������Ϊ20.90%��
��ѡC��
���� ���⿼�����Իع鷽�̵����壬���ڻ����⣮

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
7����֪������C��y2=4x�Ľ���ΪF�������������һ��P��������Ϊl1������F�Ҵ�ֱ��PF��ֱ��Ϊl2����l1��l2����Q�ĺ�����Ϊ��������
| A�� | -$\frac{3}{4}$ | B�� | -1 | C�� | -$\frac{4}{3}$ | D�� | ����ȷ�� |
5����֪a��b����ʵ������a��0��b��0����a��b���ǡ�a+lna��b+lnb���ģ�������
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��ֱ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
12��ֱ��x+$\sqrt{3}$y-2=0����б��Ϊ��������
| A�� | 30�� | B�� | 120�� | C�� | 150�� | D�� | 60�� |
6����֪����ZΪ������������z+2��2-8iҲ�Ǵ���������Z���鲿Ϊ��������
| A�� | 2 | B�� | -2 | C�� | -2i | D�� | 2��-2 |
9��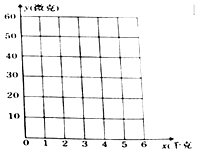 ��ũ����ʹ�õͺ�ɱ��ũҩ���߲˽����������Է�ֹ�����Σ�������ɼ�����ʱ�߲��Դ��������IJ���ũҩ��ʳ��ʱ��Ҫ����ˮ��ϴ�ɾ����±�������ˮx����λ��ǧ�ˣ� ��ϴ���߲�1ǧ�˺��߲��ϲ�����ũҩy����λ���ˣ� ��ͳ�Ʊ���
��ũ����ʹ�õͺ�ɱ��ũҩ���߲˽����������Է�ֹ�����Σ�������ɼ�����ʱ�߲��Դ��������IJ���ũҩ��ʳ��ʱ��Ҫ����ˮ��ϴ�ɾ����±�������ˮx����λ��ǧ�ˣ� ��ϴ���߲�1ǧ�˺��߲��ϲ�����ũҩy����λ���ˣ� ��ͳ�Ʊ���
��1�������������ϵ�У����ɢ��ͼ�����жϱ���x��y������ԣ�
��2�����ý���ʽ$\widehaty=c{x^2}+d$��Ϊ�߲�ũҩ����$\widehaty$����ˮ��x�Ļع鷽�̣����=x2������ƽ��ֵ$\overline��$��$\overline y$��������±������ڴ���У������$\widehaty$��x�Ļع鷽�̣���c��d��ȷ��0.1��
��3������ij�ֲ������߲��ϵ�ũҩ�������IJ���������20��ʱ����������Ϊ�˷���ʳ�ø��߲ˣ���
������Ҫ�ö���ǧ�˵���ˮ��ϴһǧ���߲ˣ�����ȷ��0.1���ο�����$\sqrt{5}��2.236$��
���������Իع鷽��$\widehaty=bx+a$��ϵ�����㹫ʽ�ֱ�Ϊ��$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{��\overline x��}^2}}}=\frac{{\sum_{i=1}^n{��{x_i}-\overline x����{y_i}-\overline y}��}}{{\sum_{i=1}^n{{{��{x_i}-\overline x��}^2}}}}$��$a=\overline y-b\overline x$��
 ��ũ����ʹ�õͺ�ɱ��ũҩ���߲˽����������Է�ֹ�����Σ�������ɼ�����ʱ�߲��Դ��������IJ���ũҩ��ʳ��ʱ��Ҫ����ˮ��ϴ�ɾ����±�������ˮx����λ��ǧ�ˣ� ��ϴ���߲�1ǧ�˺��߲��ϲ�����ũҩy����λ���ˣ� ��ͳ�Ʊ���
��ũ����ʹ�õͺ�ɱ��ũҩ���߲˽����������Է�ֹ�����Σ�������ɼ�����ʱ�߲��Դ��������IJ���ũҩ��ʳ��ʱ��Ҫ����ˮ��ϴ�ɾ����±�������ˮx����λ��ǧ�ˣ� ��ϴ���߲�1ǧ�˺��߲��ϲ�����ũҩy����λ���ˣ� ��ͳ�Ʊ���| x | 1 | 2 | 3 | 4 | 5 |
| y | 58 | 54 | 39 | 29 | 10 |
��2�����ý���ʽ$\widehaty=c{x^2}+d$��Ϊ�߲�ũҩ����$\widehaty$����ˮ��x�Ļع鷽�̣����=x2������ƽ��ֵ$\overline��$��$\overline y$��������±������ڴ���У������$\widehaty$��x�Ļع鷽�̣���c��d��ȷ��0.1��
| �� | 1 | 4 | 9 | 16 | 25 |
| y | 58 | 54 | 39 | 29 | 10 |
| ${��_i}-\overline��$ | -10 | -7 | -2 | 5 | 14 |
| ${y_i}-\overline y$ | 20 | 16 | 1 | -28 |
������Ҫ�ö���ǧ�˵���ˮ��ϴһǧ���߲ˣ�����ȷ��0.1���ο�����$\sqrt{5}��2.236$��
���������Իع鷽��$\widehaty=bx+a$��ϵ�����㹫ʽ�ֱ�Ϊ��$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{��\overline x��}^2}}}=\frac{{\sum_{i=1}^n{��{x_i}-\overline x����{y_i}-\overline y}��}}{{\sum_{i=1}^n{{{��{x_i}-\overline x��}^2}}}}$��$a=\overline y-b\overline x$��