题目内容
tan2A•tan(30°-A)+tan2Atan(60°-A)+tan(30°-A)•tan(60°-A)= .
考点:运用诱导公式化简求值
专题:计算题
分析:先对原式进行整理,然后利用正切的两角和公式分别求得tan(30°-A)+tan(60°-A)和tan(30°-A)tan(60°-A)]代入,然后利用诱导公式化简整理,求得答案.
解答:
解:原式=tan2A[tan(30°-A)+tan(60°-A)]+[tan(30°-A)tan(60°-A)]
=tan2Atan[(30°-A)+(60°-A)][1-tan(30°-A)tan(60°-A)]+[tan(30°-A)tan(60°-A)]
=tan2Atan(90°-2A)[1-tan(30°-A)tan(60°-A)]+[tan(30°-A)tan(60°-A)]
=tan2A•cot2A[1-tan(30°-A)tan(60°-A)]+[tan(30°-A)tan(60°-A)]
=1
故答案为:1
=tan2Atan[(30°-A)+(60°-A)][1-tan(30°-A)tan(60°-A)]+[tan(30°-A)tan(60°-A)]
=tan2Atan(90°-2A)[1-tan(30°-A)tan(60°-A)]+[tan(30°-A)tan(60°-A)]
=tan2A•cot2A[1-tan(30°-A)tan(60°-A)]+[tan(30°-A)tan(60°-A)]
=1
故答案为:1
点评:本题主要考查了正切的两角和公式和运用诱导公式化简求值.考查了学生对三角函数基础知识和基本公式的记忆.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
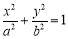 (a>b>0)的上顶点为A,左,右焦点分别为F1,F2,且椭圆C过点P(
(a>b>0)的上顶点为A,左,右焦点分别为F1,F2,且椭圆C过点P(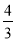 ,
,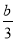 ),以AP为直径的圆恰好过右焦点F2.
),以AP为直径的圆恰好过右焦点F2.
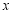 轴上是否存在两定点,使其到直线l的距离之积为1?若存在,请求出两定点坐标;若不存在,请说明理由.
轴上是否存在两定点,使其到直线l的距离之积为1?若存在,请求出两定点坐标;若不存在,请说明理由.