题目内容
(本题满分12分)已知椭圆C: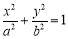 (a>b>0)的上顶点为A,左,右焦点分别为F1,F2,且椭圆C过点P(
(a>b>0)的上顶点为A,左,右焦点分别为F1,F2,且椭圆C过点P(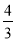 ,
,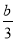 ),以AP为直径的圆恰好过右焦点F2.
),以AP为直径的圆恰好过右焦点F2.

(1)求椭圆C的方程;
(2)若动直线l与椭圆C有且只有一个公共点,试问:在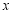 轴上是否存在两定点,使其到直线l的距离之积为1?若存在,请求出两定点坐标;若不存在,请说明理由.
轴上是否存在两定点,使其到直线l的距离之积为1?若存在,请求出两定点坐标;若不存在,请说明理由.
(1) ;(2)存在两个定点(1,0),(?1,0),使其到直线l 的距离之积为定值1
;(2)存在两个定点(1,0),(?1,0),使其到直线l 的距离之积为定值1
【解析】
试题分析:【解析】
(1)因为椭圆过点P( ,
, ),所以
),所以 ,解得
,解得 ,
,
又以AP为直径的圆恰好过右焦点 .所以A
.所以A ?
? P,即?
P,即? =?1,
=?1,  =c(4?3c). 6分
=c(4?3c). 6分
而 ,所以
,所以 ?2c+1=0,解得
?2c+1=0,解得 =1,
=1,
故椭圆C的方程是 . 4分
. 4分
(2)①当直线l斜率存在时,设直线l方程为y=kx+p,代入椭圆方程得

因为直线l与椭圆C有只有一个公共点,所以
 ,
,
即  7分
7分
设在x轴上存在两点(s,0),(t,0),使其到直线l的距离之积为1,则
 ,
,
即(st+1)k+p(s+t)=0(*),或 (**).
(**).
由(*)恒成立,得 ,解得
,解得 ,或
,或 ,
,
而(**)不恒成立. 10分
②当直线l斜率不存在时,直线方程为x=? 时,
时,
定点 (-1,0)、
(-1,0)、 (1,0)到直线l的距离之积
(1,0)到直线l的距离之积 .
.
综上,存在两个定点(1,0),(?1,0),使其到直线l 的距离之积为定值1 12分

考点:本题考查椭圆的标准方程,椭圆的几何性质,直线与椭圆的位置关系

练习册系列答案
相关题目
 与
与 的夹角是
的夹角是 ,
, ,则
,则 _________________.
_________________. 的值为( )
的值为( )

 集合
集合
 则
则 为_________________.
为_________________.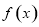 是定义在
是定义在 上恒不为零的函数,且对任意的实数
上恒不为零的函数,且对任意的实数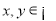 ,都有
,都有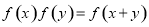 ,若
,若 ,
, ,则数列
,则数列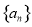 的前
的前 项和
项和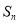 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.