题目内容
在空间中,下列正确命题的个数是( )
①若
•
=0,则
=0或
=0;
②(
•
)
=
(
•
);
③
2
2=(
•
)2;
④|
+
||
-
|=|
-
|;
⑤
与(
•
)
-(
•
)
垂直.
①若
| a |
| b |
| a |
| b |
②(
| a |
| b |
| c |
| a |
| b |
| c |
③
| p |
| q |
| p |
| q |
④|
| p |
| q |
| p |
| q |
| p |
| q |
⑤
| a |
| a |
| b |
| c |
| a |
| c |
| b |
| A、1 | B、2 | C、3 | D、4 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:结合向量的数量积的运算性质进行逐个验证即可.
解答:
解:对于选项①:若
•
=0,则
与
共线或者垂直,
如果其中有一个向量为零向量时,此时为共线,
当都不是零向量时,则满足垂直关系,故该命题为错误的;
对于选项②:(
•
)
=
(
•
);向量的数量积不满足结合律,故该命题为错误的;
对于选项③:
2
2=(
•
)2;
2
2=|
|2|
|2,
∵(
•
)2=(|
||
|cosθ)2,
∴③不成立;
对于选项④|
+
||
-
|=|
-
|;
显然错误;
对于选项⑤:
∵
•[(
•
)
-(
•
)
]
=(
•
)(
•
)-(
•
)(
•
)
=0,
∴
与(
•
)
-(
•
)
垂直.
故该命题为正确的.
综上,得到正确命题为:⑤,
故正确命题的个数为:1个,
故选:A.
| a |
| b |
| a |
| b |
如果其中有一个向量为零向量时,此时为共线,
当都不是零向量时,则满足垂直关系,故该命题为错误的;
对于选项②:(
| a |
| b |
| c |
| a |
| b |
| c |
对于选项③:
| p |
| q |
| p |
| q |
| p |
| q |
| p |
| q |
∵(
| p |
| q |
| p |
| q |
∴③不成立;
对于选项④|
| p |
| q |
| p |
| q |
| p |
| q |
显然错误;
对于选项⑤:
∵
| a |
| a |
| b |
| c |
| a |
| c |
| b |
=(
| a |
| b |
| a |
| c |
| a |
| c |
| a |
| b |
=0,
∴
| a |
| a |
| b |
| c |
| a |
| c |
| b |
故该命题为正确的.
综上,得到正确命题为:⑤,
故正确命题的个数为:1个,
故选:A.
点评:本题重点考查了平面向量的数量积的运算率、向量垂直的条件等知识,属于中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
已知函数f(x)=
是x∈(-∞,+∞)上的减函数,则a的取值范围是( )
|
A、(0,
| ||||
B、(
| ||||
| C、(2,3) | ||||
D、(
|
已知常数a、b、c都是实数,f(x)=ax3+bx2+cx-34的导函数为f′(x),f′(x)≤0的解集为{x|-2≤x≤3},若f(x)的极小值等于-115,则a的值是( )
A、-
| ||
B、
| ||
| C、2 | ||
| D、5 |
函数y=2-
的值域是( )
| -x2+4x |
| A、[-2,2] | ||||
| B、[1,2] | ||||
| C、[0,2] | ||||
D、[-
|
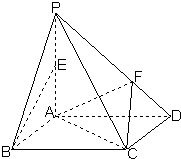 已知在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是平行四边形,E为PA的中点.
已知在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是平行四边形,E为PA的中点.