题目内容
设函数f0（x）=-sinx，f1（x）=f′0（x），f2（x）=f′1（x），…，fn+1（x）=f′n（x），n∈N*，则f2015（x）=（ ）
| A、cosx | B、-sinx |
| C、sinx | D、-cosx |
考点：导数的运算,函数的周期性
专题：导数的概念及应用
分析：由题意对函数的变化规律进行探究，发现呈周期性的变化，且其周期是4，即可得到结论．
解答：
解：由题意f0（x）=-sinx，
f1（x）=f0′（x）=-cosx，
f2（x）=f1′（x）=sinx，
f3（x）=f2′（x）=cosx，
f4（x）=f3′（x）=-sinx，
由此可知，在逐次求导的过程中，所得的函数呈周期性变化，从0开始计，周期是4，
∵2015=4×503+3，
故f2015（x）=f3（x）=cosx
故选：A．
f1（x）=f0′（x）=-cosx，
f2（x）=f1′（x）=sinx，
f3（x）=f2′（x）=cosx，
f4（x）=f3′（x）=-sinx，
由此可知，在逐次求导的过程中，所得的函数呈周期性变化，从0开始计，周期是4，
∵2015=4×503+3，
故f2015（x）=f3（x）=cosx
故选：A．
点评：本题考查函数的周期性，探究过程中用的是归纳推理，对其前几项进行研究得出规律，求解本题的关键一是要归纳推理的意识，一是对正、余弦函数的导数求法公式熟练掌握．
练习册系列答案
相关题目
已知函数f（x）=x3+x（x∈R），当0＜θ≤
时，f（msinθ）+f（sinθ-sin2θ-2）＜0恒成立，则实数m的取值范围是（ ）
| π |
| 2 |
A、（-∞，2
| ||
B、（-∞，2
| ||
| C、（-∞，3） | ||
| D、（-∞，2） |
设复数z=1+ai（a∈R，i是虚数单位），若M{x|x＞2}，使|z|∈CRM成立的a的取值范围是（ ）
A、[-
| ||||
B、[-
| ||||
| C、[-1.1] | ||||
| D、[-2.2] |
已知函数f（x）=x2-2ax+1，其中a∈R，则“a＞0”是“f〔-2013）＞f（2015）”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件． |
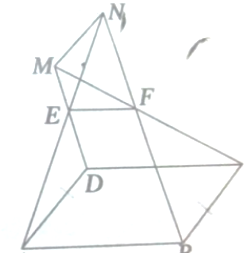如图所示，若ABCD为平行四边形，EF∥AB，AE与BF相交于点N，DE与CF相交于点M．求证：MN∥AD．