题目内容
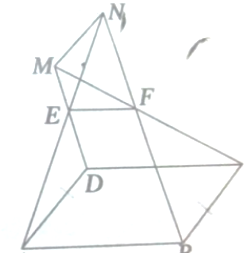如图所示，若ABCD为平行四边形，EF∥AB，AE与BF相交于点N，DE与CF相交于点M．求证：MN∥AD．考点：平面的基本性质及推论
专题：空间位置关系与距离
分析：由已知得到EF∥CD，再由平行线分线段成比例定理得到EF：AB=EN：AN，EF：CD=ME：MD，又AB=CD，得到EN：AN=ME：MD，利用平行线分线段成比例定理的判定得到所证．
解答：
证明：因为ABCD为平行四边形，所以AB∥CD，又EF∥AB，所以EF∥CD，
AE与BF相交于点N，DE与CF相交于点M．
所以EF：AB=EN：AN，EF：CD=ME：MD，又AB=CD，
所以EN：AN=ME：MD，
所以MN∥AD．
AE与BF相交于点N，DE与CF相交于点M．
所以EF：AB=EN：AN，EF：CD=ME：MD，又AB=CD，
所以EN：AN=ME：MD，
所以MN∥AD．
点评：本题考查了平行线的传递性的运用：即a/b，b∥c，则a∥c．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
设函数f0（x）=-sinx，f1（x）=f′0（x），f2（x）=f′1（x），…，fn+1（x）=f′n（x），n∈N*，则f2015（x）=（ ）
| A、cosx | B、-sinx |
| C、sinx | D、-cosx |
已知实数集R，集合A={x|0＜x＜2}，B={x∈z|x2+4≤5x}，则（∁RA）∩B=（ ）
| A、{x|2≤x≤3} |
| B、{2，3，4} |
| C、{1，2，3，4} |
| D、{x|2≤x≤4} |
某校为了解高一年级期末考试数学科的情况，从高一的所有数学试卷中随机抽取n份试卷进行分析，得到数学成绩频率分布直方图如图所示，其中成绩在[70，80）的人数为20，规定：成绩≥80分为优秀．