题目内容
【题目】已知函数![]() ,函数
,函数![]() 的图象与
的图象与![]() 的图象关于
的图象关于![]() 对称.
对称.
(1)若关于![]() 的方程
的方程![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)令![]() ,问题转化为关于
,问题转化为关于![]() 的方程
的方程![]() 在
在![]() 上有实数解,由参变量分离法得出
上有实数解,由参变量分离法得出![]() ,从而可得出实数
,从而可得出实数![]() 的取值范围即为函数
的取值范围即为函数![]() 在
在![]() 上的值域,利用二次函数的基本性质求出即可;
上的值域,利用二次函数的基本性质求出即可;
(2)求出函数![]() 的反函数
的反函数![]() 的解析式,可得出
的解析式,可得出![]() ,由题意得出
,由题意得出![]() ,利用对数函数的单调性以及真数大于零这些条件得出关于实数
,利用对数函数的单调性以及真数大于零这些条件得出关于实数![]() 的不等式组 ,解出即可.
的不等式组 ,解出即可.
(1)令![]() ,则关于
,则关于![]() 的方程
的方程![]() 在
在![]() 上有实数解,
上有实数解,
得![]() ,则实数
,则实数![]() 的取值范围即为函数
的取值范围即为函数![]() 在
在![]() 上的值域,
上的值域,
二次函数![]() 的图象开口向上,对称轴为直线
的图象开口向上,对称轴为直线![]() ,
,
所以,函数![]() 在
在![]() 上单调递增,当
上单调递增,当![]() 时,
时,![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() ;
;
(2)由题意知,函数![]() 与函数
与函数![]() 互为反函数,
互为反函数,
由![]() ,得
,得![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,
,
则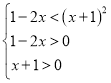 ,解得
,解得![]() ,因此,实数
,因此,实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目