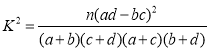题目内容
【题目】如图,椭圆![]()
![]() 的左右焦点分别为的
的左右焦点分别为的![]() 、
、![]() ,离心率为
,离心率为![]() ;过抛物线
;过抛物线![]() 焦点
焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 、
、![]() 两点,当
两点,当![]() 时,
时, ![]() 点在
点在![]() 轴上的射影为
轴上的射影为![]() 。连结
。连结![]() 并延长分别交
并延长分别交![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ;
; ![]() 与
与![]() 的面积分别记为
的面积分别记为![]() ,
, ![]() ,设
,设![]() .
.
(Ⅰ)求椭圆![]() 和抛物线
和抛物线![]() 的方程;
的方程;
(Ⅱ)求![]() 的取值范围.
的取值范围.
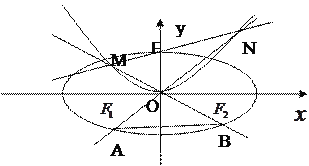
【答案】(1) ![]() ,
,![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(Ⅰ )由题意得得![]() ,根据点M在抛物线上得
,根据点M在抛物线上得![]() ,又由
,又由![]() ,得
,得 ![]() ,可得
,可得![]() ,解得
,解得![]() ,从而得
,从而得![]() ,可得曲线方程。(Ⅱ )设
,可得曲线方程。(Ⅱ )设![]() ,
, ![]() ,分析可得
,分析可得![]() ,先设出直线
,先设出直线![]() 的方程为
的方程为![]()
![]() ,由
,由![]() ,解得
,解得![]() ,从而可求得
,从而可求得![]() ,同理可得
,同理可得![]() ,故可将
,故可将![]() 化为m的代数式,用基本不等式求解可得结果。
化为m的代数式,用基本不等式求解可得结果。
试题解析:
(Ⅰ)由抛物线定义可得![]() ,
,
∵点M在抛物线![]() 上,
上,
∴![]() ,即
,即![]() ①
①
又由![]() ,得
,得 ![]()
将上式代入①,得![]()
解得![]()
∴![]()
![]() ,
,
所以曲线![]() 的方程为
的方程为![]() ,曲线
,曲线![]() 的方程为
的方程为![]() 。
。
(Ⅱ)设直线![]() 的方程为
的方程为![]() ,
,
由![]() 消去y整理得
消去y整理得![]() ,
,
设![]() ,
, ![]() .
.
则![]() ,
,
设![]() ,
, ![]() ,
,
则![]() ,
,
所以![]() , ②
, ②
设直线![]() 的方程为
的方程为![]()
![]() ,
,
由![]() ,解得
,解得![]() ,
,
所以![]() ,
,
由②可知,用![]() 代替
代替![]() ,
,
可得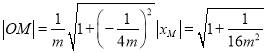 ,
,
由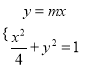 ,解得
,解得![]() ,
,
所以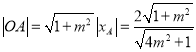 ,
,
用![]() 代替
代替![]() ,可得
,可得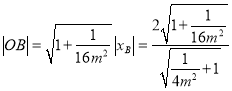
所以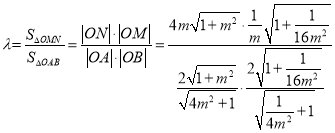
![]()
![]() ,当且仅当
,当且仅当![]() 时等号成立。
时等号成立。
所以![]() 的取值范围为
的取值范围为![]() .
.

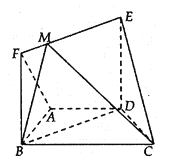
【题目】如图,四棱锥O﹣ABCD的底面是边长为1的菱形,OA=2,∠ABC=60°,OA⊥平面ABCD,M、N分别是OA、BC的中点.
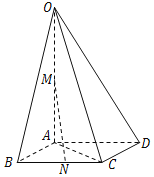
(1)求证:直线MN∥平面OCD;
(2)求点M到平面OCD的距离.
【题目】某公司![]() 人数众多
人数众多![]() 为鼓励员工利用网络进行营销,准备为员工办理手机流量套餐.为了解员工手机流量使用情况,按照男员工和女员工
为鼓励员工利用网络进行营销,准备为员工办理手机流量套餐.为了解员工手机流量使用情况,按照男员工和女员工![]() 的比例分层抽样,得到
的比例分层抽样,得到![]() 名员工的月使用流量
名员工的月使用流量![]() (单位:
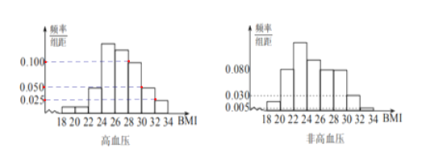
(单位:![]() )的数据,其频率分布直方图如图所示.
)的数据,其频率分布直方图如图所示.
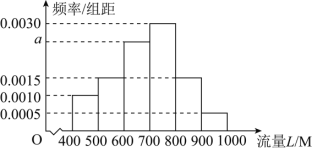
(1)求![]() 的值,并估计这
的值,并估计这![]() 名员工月使用流量的平均值
名员工月使用流量的平均值![]() (同一组中的数据用中点值代表
(同一组中的数据用中点值代表![]() ;
;
(2)若将月使用流量在![]() 以上(含
以上(含![]() )的员工称为“手机营销达人”,填写下面的
)的员工称为“手机营销达人”,填写下面的![]() 列联表,能否有超过
列联表,能否有超过![]() 的把握认为“成为手机营销达人与员工的性别有关”;
的把握认为“成为手机营销达人与员工的性别有关”;
男员工 | 女员工 | 合计 | |
手机营销达人 | 5 | ||
非手机营销达人 | |||
合计 | 200/span> |
参考公式及数据:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(3)若这![]() 名员工中有
名员工中有![]() 名男员工每月使用流量在
名男员工每月使用流量在![]() ,从每月使用流量在
,从每月使用流量在![]() 的员工中随机抽取名
的员工中随机抽取名![]() 进行问卷调查,记女员工的人数为
进行问卷调查,记女员工的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.