题目内容
已知直线l与直线2x+y-1=0垂直,且与两坐标轴围成的三角形面积为5,求直线l的方程.
考点:直线的截距式方程,直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:设要求的直线方程为x-2y+m=0.令x=0,解得y=
;令y=0,解得x=-m.可得
|
×(-m)|=5,解出即可.
| m |
| 2 |
| 1 |
| 2 |
| m |
| 2 |
解答:
解:设要求的直线方程为x-2y+m=0.
令x=0,解得y=
;令y=0,解得x=-m.
∴
|
×(-m)|=5,
解得m=±2
.
∴直线l的方程为x-2y±2
=0.
令x=0,解得y=
| m |
| 2 |
∴
| 1 |
| 2 |
| m |
| 2 |
解得m=±2
| 5 |
∴直线l的方程为x-2y±2
| 5 |
点评:本题考查了相互垂直的直线斜率之间的关系、截距式、三角形的面积计算公式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
定义在实数集R上奇函数f(x)的最小正周期为20,在区间(0,10)内方程f(x)=0有且仅有一个解x=3,则方程f(
+3)=0在[-100,400]上不同的解的个数为( )
| x |
| 4 |
| A、20 | B、25 | C、26 | D、27 |
已知集合P={x|x2-2x-3>0},Q={x|log2(x-2)<1},则(∁RP)∩Q=( )
| A、{x|2<x≤3} |
| B、{x|-1≤x≤3} |
| C、{x|3<x≤4} |
| D、{x|3<x≤4或x<-1} |
已知函数f(x)=
sin2xsinφ+cos2xcosφ-
sin(
+φ)(0<φ<π),将凼数f(x)的图象向左移
个单位后关于y轴对称,则φ等于( )
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 12 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,半径都为1的三个圆两两相交,
如图,半径都为1的三个圆两两相交, |
| AB |
 |
| BC |
 |
| AC |
 |
| CD |
| π |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
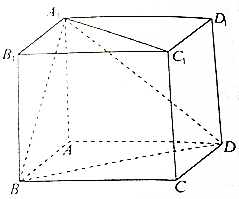 如图,正方体ABCD-A1B1C1D1的棱长为a,求:
如图,正方体ABCD-A1B1C1D1的棱长为a,求: