题目内容
设无穷等比数列{an}的公比为q,且an>0(n∈N*),[an]表示不超过实数an的最大整数(如[2.5]=2),记bn=[an],数列{an}的前n项和为Sn,数列{bn}的前n项和为Tn.
(Ⅰ)若a1=14,q=
,求T3;
(Ⅱ)证明:Sn=Tn(n=1,2,3,…)的充分必要条件为an∈N*;
(Ⅲ)若对于任意不超过2014的正整数n,都有Tn=2n+1,证明:(
)
<q<1.
(Ⅰ)若a1=14,q=
| 1 |
| 2 |
(Ⅱ)证明:Sn=Tn(n=1,2,3,…)的充分必要条件为an∈N*;
(Ⅲ)若对于任意不超过2014的正整数n,都有Tn=2n+1,证明:(
| 2 |
| 3 |
| 1 |
| 2012 |
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件推导出b1=14,b2=7,b3=3,由此能嫠出T3.
(Ⅱ)先证明充分性,由an∈N*,推导出Sn=Tn.再证明必要性:对于任意的n∈N*,Sn=Tn,推导出对一切正整数n都有an∈N*.
(Ⅲ)由已知条件推导出b1=T1=3,bn=Tn-Tn-1=2,(2≤n≤2014).a1∈[3,4),an∈[2,3),(2≤n≤2014),q<1,q2012≥
>
,由此能证明(
)
<q<1.
(Ⅱ)先证明充分性,由an∈N*,推导出Sn=Tn.再证明必要性:对于任意的n∈N*,Sn=Tn,推导出对一切正整数n都有an∈N*.
(Ⅲ)由已知条件推导出b1=T1=3,bn=Tn-Tn-1=2,(2≤n≤2014).a1∈[3,4),an∈[2,3),(2≤n≤2014),q<1,q2012≥
| 2 |
| a2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2012 |
解答:
(Ⅰ)解:∵等比数列{an}中,a1=14,q=
,
∴a1=14,a2=7,a3=3.5.…(1分)
∴b1=14,b2=7,b3=3.…(2分)
∴T3=b1+b2+b3=24.…(3分)
(Ⅱ)证明:(充分性)∵an∈N*,
∴bn=[an]=an 对一切正整数n都成立.
∵Sn=a1+a2+…+an,Tn=b1+b2+…+bn,
∴Sn=Tn.…(5分)
(必要性))∵对于任意的n∈N*,Sn=Tn,
当n=1时,由a1=S1,b1=T1,得a1=b1; …(6分)
当n≥2时,由an=Sn-Sn-1,bn=Tn-Tn-1,得an=bn.
对一切正整数n都有an=bn.…(7分)
由 bn ∈Z,an>0,得对一切正整数n都有an∈N*.…(8分)
(Ⅲ)证明:∵Tn=2n+1(n≤2014),
∴b1=T1=3,bn=Tn-Tn-1=2,(2≤n≤2014).…(9分)
∵bn=[an],
∴a1∈[3,4),an∈[2,3),(2≤n≤2014).…(10分)
由 q=
,得q<1.…(11分)
∵a2014=a2q2012∈[2,3),
∴q2012≥
>
,
∴
<q2012<1,即(
)
<q<1.…(13分)
| 1 |
| 2 |
∴a1=14,a2=7,a3=3.5.…(1分)
∴b1=14,b2=7,b3=3.…(2分)
∴T3=b1+b2+b3=24.…(3分)
(Ⅱ)证明:(充分性)∵an∈N*,
∴bn=[an]=an 对一切正整数n都成立.
∵Sn=a1+a2+…+an,Tn=b1+b2+…+bn,
∴Sn=Tn.…(5分)
(必要性))∵对于任意的n∈N*,Sn=Tn,
当n=1时,由a1=S1,b1=T1,得a1=b1; …(6分)
当n≥2时,由an=Sn-Sn-1,bn=Tn-Tn-1,得an=bn.
对一切正整数n都有an=bn.…(7分)
由 bn ∈Z,an>0,得对一切正整数n都有an∈N*.…(8分)
(Ⅲ)证明:∵Tn=2n+1(n≤2014),
∴b1=T1=3,bn=Tn-Tn-1=2,(2≤n≤2014).…(9分)
∵bn=[an],
∴a1∈[3,4),an∈[2,3),(2≤n≤2014).…(10分)
由 q=
| a2 |
| a1 |
∵a2014=a2q2012∈[2,3),
∴q2012≥
| 2 |
| a2 |
| 2 |
| 3 |
∴
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2012 |
点评:本题考查数列的前3项和的求法,考查等式成立的充要条件的证明,考查不等式的证明,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
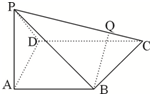 四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=AD=
四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=AD=