题目内容
当a>-1时,解不等式x2-(a+1)x-2a2-a≥0.
考点:一元二次不等式的解法
专题:分类讨论,不等式的解法及应用
分析:把不等式x2-(a+1)x-2a2-a≥0化为(x+a)[x-(2a+1)]≥0,讨论a的取值,写出对应不等式的解集.
解答:
解:不等式x2-(a+1)x-2a2-a≥0可化为
(x+a)[x-(2a+1)]≥0,
∵a>-1,∴-a<1,2a+1>-1;
当-a=2a+1,即a=-
时,不等式的解集是R;
当-a>2a+1,即-1<a<-
时,不等式的解集是{x|x≤2a+1,或x≥-a};
当-a<2a+1,即a>-
时,不等式的解集是{x|x≤-a,或x≥2a+1}.
∴a=-
时,不等式的解集是R;
-1<a<-
时,不等式的解集是{x|x≤2a+1,或x≥-a};
a>-
时,不等式的解集是{x|x≤-a,或x≥2a+1}.
(x+a)[x-(2a+1)]≥0,
∵a>-1,∴-a<1,2a+1>-1;
当-a=2a+1,即a=-
| 1 |
| 3 |
当-a>2a+1,即-1<a<-
| 1 |
| 3 |
当-a<2a+1,即a>-
| 1 |
| 3 |
∴a=-
| 1 |
| 3 |
-1<a<-
| 1 |
| 3 |
a>-
| 1 |
| 3 |
点评:本题考查了含有字母系数的不等式的解法问题,解题时应在适当地时候,对字母系数进行讨论,是基础题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
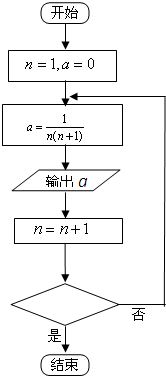 执行如图程序框图:
执行如图程序框图: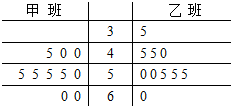 某校随机抽取某次高三数学模拟考试甲、乙两班各10名同学的客观题成绩(满分60分),统计后获得成绩数据的茎叶图(以十位数字为茎,个位数字为叶),如图所示:
某校随机抽取某次高三数学模拟考试甲、乙两班各10名同学的客观题成绩(满分60分),统计后获得成绩数据的茎叶图(以十位数字为茎,个位数字为叶),如图所示: