题目内容
已知命题p:方程(ax+2)(ax+1)=0在[-1,1]上有解;命题p:不等式x2﹢2ax﹢2a≥0恒成立;若命题“p∨q”是假命题,求a的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:分别求出命题p,q为真命题的等价条件,利用复合命题之间的关系即可得到结论.
解答:
解:若a=0,则方程(ax+2)(ax+1)=0不成立,即a≠0,
则方程(ax+2)(ax+1)=0的两个根为-
或-
,
若方程(ax+2)(ax+1)=0在[-1,1]上有解,
则-1≤-
≤1或-1≤-
≤1,
则a≥2或a≤-2,
若不等式x2﹢2ax﹢2a≥0恒成立,则△=4a2-8a≤0,
解得0≤a≤2,
若p∨q为假命题,则p,q同时为假命题,即
,
即-2<a<0
则方程(ax+2)(ax+1)=0的两个根为-
| 2 |
| a |
| 1 |
| a |
若方程(ax+2)(ax+1)=0在[-1,1]上有解,
则-1≤-
| 2 |
| a |
| 1 |
| a |
则a≥2或a≤-2,
若不等式x2﹢2ax﹢2a≥0恒成立,则△=4a2-8a≤0,
解得0≤a≤2,
若p∨q为假命题,则p,q同时为假命题,即
|
即-2<a<0
点评:本题主要考查复合命题的真假关系的应用,比较基础.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
设集合A={x|x2-3x=0,x∈R},B={x|x2+3x=0,x∈R},则A∩B=( )
| A、{0} |
| B、{0,-3} |
| C、{0,3} |
| D、{0,-3,3} |
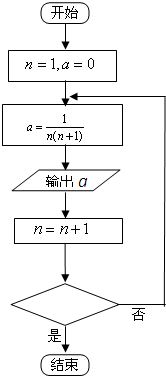 执行如图程序框图:
执行如图程序框图: