题目内容
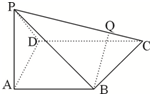 四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=AD=
四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=AD=| 1 |
| 2 |
(1)在侧棱PC上是否存在一点Q,使BQ∥面PAD?说明理由.
(2)设M为PC中点,PA=1,求P-ABM体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的性质
专题:空间位置关系与距离
分析:(1)存在点Q为PC中点时,满足BQ∥面PAD;证明当Q为PC的中点时,BQ∥平面PAD即可;
(2)利用等积法求出三棱锥P-ABM的体积.
(2)利用等积法求出三棱锥P-ABM的体积.
解答:
解:(1)存在点Q为PC中点时,满足BQ∥面PAD;
证明:延长DA交CB延长线于E,连接PE,
∴B为EC中点;
当Q为PC的中点时,BQ∥PE;
又BQ?面PAD,PE?面PAD,
∴BQ∥平面PAD;
(2)三棱锥P-ABM的体积为
V三棱锥P-ABM=V三棱锥B-PAM
=
V三棱锥B-PAC=
V三棱锥P-ABC
=
×
×1×1×
×1=
.
证明:延长DA交CB延长线于E,连接PE,
∴B为EC中点;
当Q为PC的中点时,BQ∥PE;
又BQ?面PAD,PE?面PAD,
∴BQ∥平面PAD;
(2)三棱锥P-ABM的体积为
V三棱锥P-ABM=V三棱锥B-PAM
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 12 |
点评:本题考查了空间中的线面平行的判定问题以及求锥体的体积问题,解题时应明确线面平行的条件是什么,锥体的体积公式是什么,以便灵活地解答问题.

练习册系列答案
相关题目
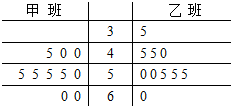 某校随机抽取某次高三数学模拟考试甲、乙两班各10名同学的客观题成绩(满分60分),统计后获得成绩数据的茎叶图(以十位数字为茎,个位数字为叶),如图所示:
某校随机抽取某次高三数学模拟考试甲、乙两班各10名同学的客观题成绩(满分60分),统计后获得成绩数据的茎叶图(以十位数字为茎,个位数字为叶),如图所示: