题目内容
9.函数f(x)满足:对?x∈R+都有f′(x)=$\frac{3}{x}$f(x),且f(22016)≠0,则$\frac{f({2}^{2017})}{f({2}^{2016})}$的值为( )| A. | 0.125 | B. | 0.8 | C. | 1 | D. | 8 |
分析 构造函数g(x)=$\frac{f(x)}{{x}^{3}}$,得到f(x)=cx3,代值计算即可.
解答 解:∵f′(x)=$\frac{3}{x}$f(x),
∴xf′(x)-3f(x)=0,
设g(x)=$\frac{f(x)}{{x}^{3}}$,
∴g′(x)=$\frac{{x}^{3}f′(x)-3{x}^{2}f(x)}{{x}^{6}}$=$\frac{{x}^{2}[xf′(x)-3f(x)]}{{x}^{6}}$=0,
∴g(x)=c,(c常数),
∴f(x)=cx3,
∴$\frac{f({2}^{2017})}{f({2}^{2016})}$=$\frac{c({2}^{2017})^{3}}{c({2}^{2016})^{3}}$=23=8,
故选:D
点评 本题考查了导数的运算和函数值的求法,关键是构造函数,属于中档题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.设函数f(x)在(-∞,+∞)上有意义,对于给定的正数k,定义函数fk(x)=$\left\{\begin{array}{l}{f(x),f(x)<k}\\{k,f(x)≥k}\end{array}\right.$取k=3,f(x)=($\frac{k}{2}$)|x|,则fk(x)=$\frac{k}{2}$的零点有( )
| A. | 0个 | B. | 1个 | ||
| C. | 2个 | D. | 不确定,随k的变化而变化 |
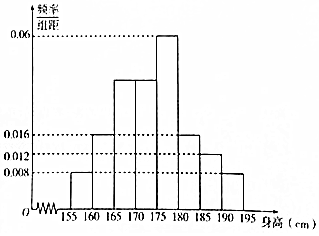 从某校高一年级1000名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米到195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如图所示.
从某校高一年级1000名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米到195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如图所示.