题目内容
函数y=Asin（ωx+φ）在一个周期内的图象如图，求此函数的解析式．
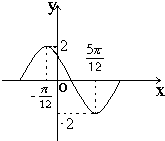
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：直接由函数图象得到A和函数的半周期，由周期公式求得ω，再由五点作图的第二点求得φ，则函数解析式可求．
解答：
解：由图可知，A=2，
=
-(-
)=
，
∴T=π，
∴ω=
=
=2．
由五点作图的第二点得，2×(-
)+φ=
，
解得：φ=
．
∴函数解析式为：y=2sin（2x+
）．
| T |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
| π |
| 2 |
∴T=π，
∴ω=
| 2π |
| T |
| 2π |
| π |
由五点作图的第二点得，2×(-
| π |
| 12 |
| π |
| 2 |
解得：φ=
| 2π |
| 3 |
∴函数解析式为：y=2sin（2x+
| 2π |
| 3 |
点评：本题考查利用y=Asin（ωx+φ）的部分图象求函数解析式，关键是掌握运用五点作图的某一点求φ，是中档题．
练习册系列答案
相关题目
极坐标系中，过点（2，
）且与极轴垂直的直线方程为（ ）
| π |
| 3 |
A、ρsinθ=-
| ||
B、ρ=-
| ||
| C、ρ=-4cosθ | ||
| D、ρcosθ-1=0 |
函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
）的部分图象如图所示，则（ ）
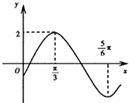
| π |
| 2 |
A、ω=1，φ=
| ||
B、ω=1，φ=-
| ||
C、ω=2，φ=
| ||
D、ω=2，φ=-
|
如图，在三棱锥P-ABC中，PC⊥底面ABC，AB⊥BC，D，E分别是AB，PB的中点．PC=1，BC=1．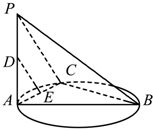
如图，已知AB是圆的直径，PA垂直圆所在的平面，C是圆上任一点，D是线段PA的中点，E是线段AC上的一点．
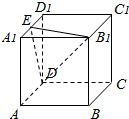正方体ABCD-A1B1C1D1的棱长为a，点E是A1D1的中点，求点A1到平面B1DE的距离．