题目内容
已知点M（1，0），N（0，1），P（2，1），Q（1，y），且
∥
，求y的值，并求出向量
的坐标．
| MN |
| PQ |
| PQ |
考点：平面向量共线（平行）的坐标表示
专题：平面向量及应用
分析：由点的坐标求出两个向量
，
的坐标，然后直接利用向量共线的坐标表示列式求得y的值，则向量
的坐标可求．
| MN |
| PQ |
| PQ |
解答：
解：∵点M（1，0），N（0，1），P（2，1），Q（1，y），
∴
=（-1，1），
=（-1，y-1）．
∵
∥
，
∴（-1）×（y-1）-1×（-1）=0，
解得y=2．
∴
=（-1，1）．
∴
| MN |
| PQ |
∵
| MN |
| PQ |
∴（-1）×（y-1）-1×（-1）=0，
解得y=2．
∴
| PQ |
点评：平行问题是一个重要的知识点，在高考题中常常出现，常与向量的模、向量的坐标表示等联系在一起，要特别注意垂直与平行的区别．若
=（a1，a2），
=（b1，b2），则
⊥
?a1a2+b1b2=0，
∥
?a1b2-a2b1=0．是基础题．
| a |
| b |
| a |
| b |
| a |
| b |
练习册系列答案
相关题目
乒乓球运动员10人，其中男女运动员各5人，从这10名运动员中选出4人进行男女混合双打比赛，选法种数为（ ）
A、（A
| ||||
B、（C
| ||||
C、（C
| ||||
D、（C
|
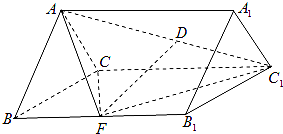如图，正三棱柱ABC-A1B1C1的各棱长都等于2，D在AC1上，F为BB1中点，且FD⊥AC1．
如图，已知AB⊥平面α于B，DC?α，且CD⊥AC于C，求证：平面ACD⊥平面ABC．
如图，四棱柱ABCD-A1B1C1D1中，平面A1ABB1⊥平面ABCD，且∠ABC=