Question

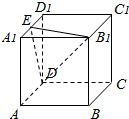正方体ABCD-A₁B₁C₁D₁的棱长为a，点E是A₁D₁的中点，求点A₁到平面B₁DE的距离．

Answer 1

考点：点、线、面间的距离计算

专题：计算题,空间位置关系与距离

分析：转换底面，利用VA-A1B1E=VA1-B1DE，可求点A₁到平面B₁DE的距离．

解答： 解：△B₁DE中，DE=B₁E=

5

2

a，B₁D=

3

a，
∴B₁D边上的高为

2

2

a，
∴S_△B1DE=

1

2

•

3

a•

2

2

a=

6

4

a²，
设点A₁到平面B₁DE的距离为h，则
∵VA-A1B1E=VA1-B1DE，
∴

1

3

•

1

2

a•

a

2

=

1

3

•

6

4

a²•h，
∴h=

6

6

．

点评：求点面距离，通常利用等体积法，注意底面的转换．