题目内容
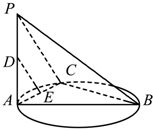 如图,已知AB是圆的直径,PA垂直圆所在的平面,C是圆上任一点,D是线段PA的中点,E是线段AC上的一点.
如图,已知AB是圆的直径,PA垂直圆所在的平面,C是圆上任一点,D是线段PA的中点,E是线段AC上的一点.求证:(Ⅰ)若E为线段AC中点,则DE∥平面PBC;
(Ⅱ)无论E在AC何处,都有BC⊥DE.
考点:直线与平面平行的判定,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(Ⅰ)由三角形中位线定理可得DE∥BC,进而由线面平行的判定定理得到DE∥平面PBC;
(Ⅱ)要证明“无论E在AC何处,都有BC⊥DE”,问题转化为证明BC⊥平面PAC.
(Ⅱ)要证明“无论E在AC何处,都有BC⊥DE”,问题转化为证明BC⊥平面PAC.
解答:
解:(Ⅰ)∵D、E分别为AB、AC中点,
∴DE∥BC.
∵DE?平面PBC,BC?平面PBC,
∴DE∥平面PBC;
(Ⅱ)∵AB是圆的直径,C是圆上任一点,
∴BC⊥AC,
又∵PA垂直圆所在的平面,
∴BC⊥PA,
又∵AC∩PA=A,
∴BC⊥平面PAC,
∵DE?平面PAC,
∴无论E在AC何处,都有BC⊥DE.
∴DE∥BC.
∵DE?平面PBC,BC?平面PBC,
∴DE∥平面PBC;
(Ⅱ)∵AB是圆的直径,C是圆上任一点,
∴BC⊥AC,
又∵PA垂直圆所在的平面,
∴BC⊥PA,
又∵AC∩PA=A,
∴BC⊥平面PAC,
∵DE?平面PAC,
∴无论E在AC何处,都有BC⊥DE.
点评:本题考查的知识点是直线与平面平行的判定,直线与平面垂直的判定,熟练掌握空间直线与平面位置关系的判定,性质是解答本题的关键,

练习册系列答案
相关题目
下列函数中,导函数是奇函数的是( )
| A、y=sinx | ||
| B、y=ex | ||
| C、y=lnx | ||
D、y=cosx-
|
已知向量
=(0,1),
=(1,0),
=(3,4),若λ为实数,且(
+λ
)⊥
,则λ的值为( )
| a |
| b |
| c |
| b |
| a |
| c |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
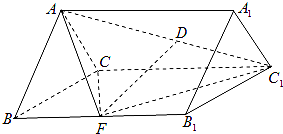 如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1.
如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1.
 如图,已知AB⊥平面α于B,DC?α,且CD⊥AC于C,求证:平面ACD⊥平面ABC.
如图,已知AB⊥平面α于B,DC?α,且CD⊥AC于C,求证:平面ACD⊥平面ABC. 如图,四棱柱ABCD-A1B1C1D1中,平面A1ABB1⊥平面ABCD,且∠ABC=
如图,四棱柱ABCD-A1B1C1D1中,平面A1ABB1⊥平面ABCD,且∠ABC=