题目内容
设m,n∈R且n≤6,若不等式2mx+(2-x)n-8≥0对任意x∈[-4,2]都成立,则
取值范围是 .
| m2+n2 |
| mn |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:将y整理成x的一次函数的形式,得到满足m,n的可行域,从而求出
的范围,进而得到代数式
的范围.
| n |
| m |
| m2+n2 |
| mn |
解答:
解:解:设y=2xm+(2-x)n-8,整理可得y=﹙2m-n﹚x+﹙2n-8﹚
当2m-n>0时,因为x∈[-4,2],所以ymin=﹙2m-n﹚•﹙-4﹚+﹙2n-8﹚=-8m+6n-8
当2m-n<0时,因为x∈[-4,2],所以ymin=﹙2m-n﹚•2+﹙2n-8﹚=4m-8
∵不等式2xm+(2-x)n-8≥0对任意x∈[-4,2]都成立,
∴m,n满足
或
,
可行域如图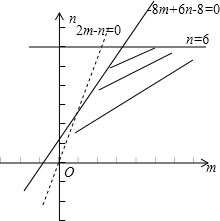 或
或
∴当且仅当m=2,n=6时,(
)max=3,∴0<
≤3,
令y=
=
+
,
令
=x,∴y=x+
,(0<x≤3),
∴2≤y≤
,
故答案为:[2,
].
当2m-n>0时,因为x∈[-4,2],所以ymin=﹙2m-n﹚•﹙-4﹚+﹙2n-8﹚=-8m+6n-8
当2m-n<0时,因为x∈[-4,2],所以ymin=﹙2m-n﹚•2+﹙2n-8﹚=4m-8
∵不等式2xm+(2-x)n-8≥0对任意x∈[-4,2]都成立,
∴m,n满足
|
|
可行域如图
 或
或
∴当且仅当m=2,n=6时,(
| n |
| m |
| n |
| m |
令y=
| m2+n2 |
| mn |
| n |
| m |
| m |
| n |
令
| n |
| m |
| 1 |
| x |
∴2≤y≤
| 10 |
| 3 |
故答案为:[2,
| 10 |
| 3 |
点评:本题考查了不等式的解法,考查了线性规划问题,考查了转化思想,是一道中档题.

练习册系列答案
相关题目
