题目内容
已知奇函数f（x）在（0，+∞）单调递增，且f（3）=0，则不等式（2x-1）•f（x）＞0的解集是 ．
考点：函数单调性的性质
专题：计算题,作图题,函数的性质及应用
分析：由题意作出f（x）的简图，化（2x-1）•f（x）＞0为
或
，从而解得．
|
|
解答：
解：由题意，可作出f（x）的简图如下：
则（2x-1）•f（x）＞0可化为
或
，
解得，x＞3或0＜x＜
或x＜-3；
故答案为：{x|x＞3或0＜x＜
或x＜-3}．
则（2x-1）•f（x）＞0可化为
|
|
解得，x＞3或0＜x＜
| 1 |
| 2 |
故答案为：{x|x＞3或0＜x＜
| 1 |
| 2 |
点评：本题考查了学生的作图能力及不等式的转化，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
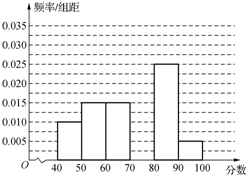从参加高二年级期中考试的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六段[40，50），[50，60），…，[90，100]后得到如下部分频率分布直方图．观察图形的信息，回答下列问题：