题目内容
f（x）是R上的奇函数，当x＞0时，f（x）=x2+x+2，则f（x）= ．
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：利用奇函数的性质可得x＜0的解析式，而f（0）=0，即可得出．
解答：
解：设x＜0，则-x＞0，．
∵x＞0，f（x）=x2+x+2，
∴f（x）=-f（-x）=-（x2-x+2）=-x2+x-2．
又f（0）=0．
故答案为：f（x）=
．
∵x＞0，f（x）=x2+x+2，
∴f（x）=-f（-x）=-（x2-x+2）=-x2+x-2．
又f（0）=0．
故答案为：f（x）=
|
点评：本题考查了函数奇偶性的应用，即根据奇偶性对应的关系式，将所求的函数解析式进行转化，转化到已知范围内进行求解，考查了转化思想．
练习册系列答案
名校课堂系列答案
相关题目
已知全集U={1，2，3，4，5}，集合A={1，2，3}，则∁UA=（ ）
| A、{4，5} |
| B、{1，2，3} |
| C、{5} |
| D、{2，4} |
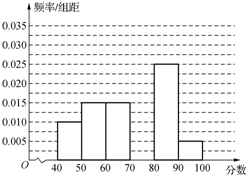从参加高二年级期中考试的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六段[40，50），[50，60），…，[90，100]后得到如下部分频率分布直方图．观察图形的信息，回答下列问题：