Question

假设关于某设备的使用年限x（年）和所支出的维修费用y（万元）有如下的统计资料：

x	2	3	4	5	6
y	2.2	3.8	5.5	6.5	7.0

（1）画出散点图并判断是否线性相关；
（2）如果线性相关，求线性回归方程；
（3）估计使用年限为10年时，维修费用是多少？

Answer 1

考点：线性回归方程

专题：应用题,概率与统计

分析：（1）利用描点法可得图象；
（2）根据所给的数据，做出变量x，y的平均数，再求出a，b的值，即可求线性回归方程；
（3）当自变量为10时，代入线性回归方程，求出维修费用，这是一个预报值．

解答： 解：（1）作散点图如下：

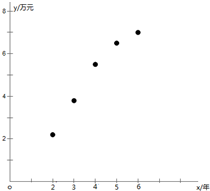
由散点图可知是线性相关的…（3分）
（2）根据题意列表如下：

i	1	2	3	4	5
xi	2	3	4	5	6
yi	2.2	3.8	5.5	6.5	7.0
xiyi	4.4	11.4	22.0	32.5	42.0
. x =4， . y =5， 5 i=1 xi2=90， 5 i=1 xiyi=112.3

…（5分）
计算得：

?

b

=

5 i=1 xiyi-5 . x . y

5 i=1 x 2 i -5 . x2

=

112.3-5×4×5

90-5×42

=1.23…（7分）
于是可得：a=5-1.23×4=0.08…（8分）
即得线性回归方程为：y═1.23x+0.08…（10分）
（3）x=10时，预报维修费用是y=1.23×10+0.08=12.3，
因此估计使用10年维修费用为12.38万元…（12分）

点评：本题考查线性回归方程的求解和应用，是一个基础题，解题的关键是正确应用最小二乘法来求线性回归方程的系数．