Question

已知函数f（x）=

1

2

+

1

2

cos（2x+

π

6

），g（x）=1+

1

2

sin2x．
（1）设x₀是y=f（x）图象最高点的横坐标，求g（2x₀）的值；
（2）令h（x）=f（x-

5π

12

）+g（x-

π

12

），若方程h（x）+k=0在[0，

π

2

]只有一个解，求实数k的取值范围．

Answer 1

考点：两角和与差的余弦函数,函数的零点,三角函数的最值

专题：三角函数的求值

分析：（1）由题意可得2x₀+

π

6

=kπ，k∈z，求得2x₀的值，可得 g（2x₀）的值．
（2）由题意利用两角和差正弦、余弦公式求得函数h（x）=

3

2

+sin（2x-

π

6

），且函数h（x）的图象和直线y=-k在[0，

π

2

]上只有一个交点．根据2x-

π

6

∈[-

π

6

，

5π

6

]，h（x）∈[1，

5

2

]，再结合h（x）在[0，

π

2

]上的图象，可得k的值．

解答： 解：（1）设x₀是y=f（x）图象最高点的横坐标，
则有2x₀+

π

6

=kπ，k∈z，求得2x₀=kπ-

π

6

，
∴g（2x₀）=1+

1

2

sin2（kπ-

π

6

）=1+

1

2

sin（-

π

3

）=1-

1

2

•

3

2

=1-

3

4

．
（2）由题意可得函数h（x）=

1

2

+

1

2

cos[2（x-

5π

12

）+

π

6

]+1+

1

2

sin2（x-

π

12

）=

3

2

+

1

2

cos（2x-

2π

3

）+

1

2

sin（2x-

π

6

）
=

3

2

+

1

2

[cos2xcos

2π

3

+sin2xsin

2π

3

]+

1

2

[sin2xcos

π

6

-cos2xsin

π

6

]
=

3

2

+

3

2

sin2x-

1

2

cos2x=

3

2

+sin（2x-

π

6

），
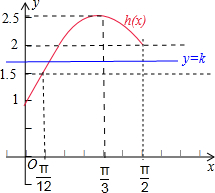
且函数h（x）的图象和直线y=-k在[0，

π

2

]上只有一个交点．
在[0，

π

2

]上，2x-

π

6

∈[-

π

6

，

5π

6

]，h（x）∈[1，

5

2

]，
再结合h（x）在[0，

π

2

]上的图象，可得-k=

5

2

，或1≤-k＜2，
求得k=-

5

2

，或-2＜k≤-1．

点评：本题主要考查两角和差余弦公式、正弦函数的图象特征，正弦函数的定义域和值域，函数的零点与方程的根的关系，属于中档题题．